Konvoluce

Konvoluce je korelační funkce f (τ) s obrácenou funkcí g (t-τ).

Operátor konvoluce je symbol hvězdičky * .

Konvoluce f (t) a g (t) se rovná integrálu f (τ) krát f (t-τ):

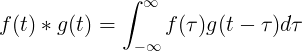
$f (t) * g (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) d \ tau$

Konvoluce 2 samostatných funkcí je definována jako:

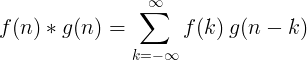
$f (n) * g (n) = \ sum_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)$

Pro zpracování obrazu se obvykle používá dvourozměrná diskrétní konvoluce.

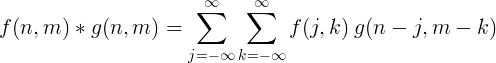
$f (n, m) * g (n, m) = \ sum_ {j = - \ infty} ^ {\ infty} \ sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: g (nj, mk)$

Diskrétní vstupní signál x (n) můžeme filtrovat konvolucí s impulsní odezvou h (n), abychom získali výstupní signál y (n).

y ( n ) = x ( n ) * h ( n )

Fourierova transformace násobení 2 funkcí se rovná konvoluci Fourierových transformací každé funkce:

ℱ { f ⋅ g } = ℱ { f } * ℱ { g }

Fourierova transformace konvoluce 2 funkcí se rovná násobení Fourierových transformací každé funkce:

ℱ { f * g } = ℱ { f } ⋅ ℱ { g }

ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )

ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )

ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )

ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )

Viz také