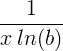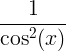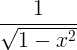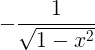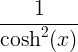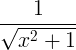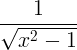Odvozená pravidla
Odvozená pravidla a zákony. Tabulka derivací funkcí.
Derivační definice
Derivací funkce je poměr rozdílu hodnoty funkce f (x) v bodech x + Δx a x s Δx, když je Δx nekonečně malý. Derivací je sklon funkce nebo sklon tečny v bodě x.
![]()
Druhá derivace
Druhá derivace je dána vztahem:
![]()
Nebo jednoduše odvodit první derivaci:
![]()
N-tý derivát
N th derivát se vypočítá odvození f (x) n-krát.
K n th derivát se rovná derivát (n-1) derivát:
f ( n ) ( x ) = [ f ( n -1) ( x )] '
Příklad:
Najděte čtvrtou derivaci
f ( x ) = 2 x 5
f (4) ( x ) = [2 x 5 ] '' '= [10 x 4 ]' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x
Derivace na grafu funkce
Derivací funkce je slop tangenciální čáry.
Odvozená pravidla
| Pravidlo odvozené částky | ( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x ) |
| Pravidlo odvozeného produktu | ( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| Derivační pravidlo kvocientu | 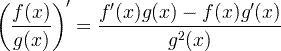 |
| Pravidlo odvozeného řetězce | f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
Pravidlo odvozené částky
Když a a b jsou konstanty.
( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Příklad:
Najděte derivaci:
3 x 2 + 4 x.
Podle pravidla součtu:
a = 3, b = 4
f ( x ) = x 2 , g ( x ) = x
f ' ( x ) = 2 x , g' ( x ) = 1
(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4
Pravidlo odvozeného produktu
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Derivační pravidlo kvocientu
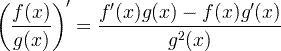
Pravidlo odvozeného řetězce
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
Toto pravidlo lze lépe pochopit pomocí Lagrangeovy notace:
![]()
Funkce lineární aproximace
Pro malé Δx můžeme získat aproximaci f (x 0 + Δx), když známe f (x 0 ) a f '(x 0 ):
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x
Tabulka derivací funkcí
| Název funkce | Funkce | Derivát |
|---|---|---|
| f ( x ) |
f '( x ) | |
| Konstantní | konst |
0 |
| Lineární | x |
1 |
| Napájení | x a |
sekera a- 1 |
| Exponenciální | e x |
e x |
| Exponenciální | a x |
a x ln a |
| Přirozený logaritmus | ln ( x ) |
|
| Logaritmus | log b ( x ) |
|
| Sinus | hřích x |
cos x |
| Kosinus | cos x |
-sin x |
| Tečna | opálení x |
|
| Arcsine | arcsin x |
|
| Arckosin | arccos x |
|
| Arkustangens | arctan x |
|
| Hyperbolický sinus | sinh x |
cosh x |
| Hyperbolický kosinus | cosh x |
sinh x |
| Hyperbolická tečna | tanh x |
|
| Inverzní hyperbolický sinus | sinh -1 x |
|
| Inverzní hyperbolický kosinus | cosh -1 x |
|
| Inverzní hyperbolická tečna | tanh -1 x |
|
Derivativní příklady
Příklad č. 1
f ( x ) = x 3 +5 x 2 + x +8
f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
Příklad č. 2
f ( x ) = hřích (3 x 2 )
Při použití pravidla řetězu:
f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x
Druhý derivační test
Když je první derivace funkce v bodě x 0 nula .
f '( x 0 ) = 0
Potom druhá derivace v bodě x 0 , f '' (x 0 ), může indikovat typ tohoto bodu:
| f '' ( x 0 )/ 0 |
místní minimum |
| f '' ( x 0 ) <0 |
místní maximum |
| f '' ( x 0 ) = 0 |
neurčeno |