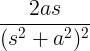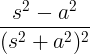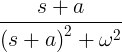Laplaceova transformace

Laplaceova transformace převádí funkci časové domény na funkci s-domény integrací z nuly do nekonečna

funkce časové domény, vynásobeno e ^-st .

Laplaceova transformace se používá k rychlému nalezení řešení pro diferenciální rovnice a integrály.

Odvození v časové doméně je transformováno na násobení s v s-doméně.

Integrace v časové doméně se transformuje na dělení s v s-doméně.

Funkce Laplaceovy transformace

Laplaceova transformace je definována operátorem L {}:

$F (s) = \ mathcal {L} \ vlevo \ {f (t) \ vpravo \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

Inverzní Laplaceovu transformaci lze vypočítat přímo.

Obvykle je inverzní transformace dána z tabulky transformací.

Název funkce	Funkce časové domény	Laplaceova transformace
Název funkce	f ( t )	F ( s ) = L { f ( t )}
Konstantní	1	$\ frac {1} {s}$
Lineární	t	$\ frac {1} {s ^ 2}$
Napájení	t ⁿ	$\ frac {n!} {s ^ {n + 1}}$
Napájení	t ^a	Γ ( a +1) ⋅ s ^{- ( a +1)}
Exponent	e ^v	$\ frac {1} {sa}$
Sinus	hřešit na	$\ frac {a} {s ^ 2 + a ^ 2}$
Kosinus	protože v	$\ frac {s} {s ^ 2 + a ^ 2}$
Hyperbolický sinus	sinh ve společnosti	$\ frac {a} {s ^ 2-a ^ 2}$
Hyperbolický kosinus	cosh ve společnosti	$\ frac {s} {s ^ 2-a ^ 2}$
Rostoucí sinus	t sin na	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Rostoucí kosinus	t cos ve	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Rozkládající se sinus	e ^-at sin ωt	$\ frac {\ omega} {\ vlevo (s + a \ vpravo) ^ 2 + \ omega ^ 2}$
Rozkládající se kosinus	e ^-at cos ωt	$\ frac {s + a} {\ vlevo (s + a \ vpravo) ^ 2 + \ omega ^ 2}$
Funkce Delta	δ ( t )	1
Zpožděná delta	δ ( ta )	e- ^jako

Název vlastnosti	Funkce časové domény	Laplaceova transformace	Komentář
	f ( t )	F ( s )
Linearita	af ( t ) + bg ( t )	aF ( s ) + bG ( s )	a , b jsou konstantní
Změna měřítka	f ( zavináč )	$\ frac {1} {a} F \ vlevo (\ frac {s} {a} \ vpravo)$	a / 0
Posun	e ^-at f ( t )	F ( s + a )
Zpoždění	f ( ta )	e ^{- jako} F ( s )
Derivace	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
N-tý derivát	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
Napájení	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Integrace	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F$
Reciproční	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
Konvoluce	f ( t ) * g ( t )	F ( s ) ⋅ G ( s )	* je operátor konvoluce
Periodická funkce	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$