Rozptyl

V pravděpodobnosti a statistice je rozptyl náhodné proměnné průměrnou hodnotou vzdálenosti čtverce od střední hodnoty. Představuje to, jak je náhodná proměnná distribuována poblíž střední hodnoty. Malá odchylka znamená, že náhodná proměnná je distribuována poblíž střední hodnoty. Velká odchylka naznačuje, že náhodná proměnná je distribuována daleko od střední hodnoty. Například při normálním rozdělení bude mít úzká křivka zvonku malou odchylku a široká křivka zvonku bude mít velkou odchylku.

Definice odchylky

Rozptyl náhodné proměnné X je očekávaná hodnota čtverců rozdílu X a očekávaná hodnota μ.

σ 2 = Var ( X ) = E [( X - μ ) 2 ]

Z definice rozptylu můžeme dostat

σ 2 = Var ( X ) = E ( X 2 ) - μ 2

Rozptyl spojité náhodné proměnné

Pro spojitou náhodnou veličinu se střední hodnotou μ a funkcí hustoty pravděpodobnosti f (x):

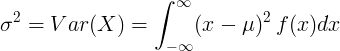
\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx

nebo

Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2

Rozptyl diskrétní náhodné proměnné

Pro diskrétní náhodnou proměnnou X se střední hodnotou μ a pravděpodobnostní hromadnou funkcí P (x):

\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)

nebo

Var (X) = \ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2

Vlastnosti rozptylu

Když X a Y jsou nezávislé náhodné proměnné:

Var ( X + Y ) = Var ( X ) + Var ( Y )

 

Směrodatná odchylka ►

 

Viz také

PRAVDĚPODOBNOST A STATISTIKA
RYCHLÉ STOLY