Rozdělení pravděpodobnosti
V pravděpodobnosti a statistika distribuce je charakteristické náhodné proměnné, popisuje pravděpodobnosti náhodné proměnné v každé hodnoty.
Každé rozdělení má určitou funkci hustoty pravděpodobnosti a funkci rozdělení pravděpodobnosti.
Ačkoli existuje neurčitý počet rozdělení pravděpodobnosti, používá se několik běžných rozdělení.
Funkce kumulativní distribuce
Rozdělení pravděpodobnosti je popsáno kumulativní distribuční funkcí F (x),
což je pravděpodobnost, že náhodná proměnná X získá hodnotu menší nebo rovnou x:
F ( x ) = P ( X ≤ x )
Kontinuální distribuce
Kumulativní distribuční funkce F (x) se vypočítá integrací funkce hustoty pravděpodobnosti f (u) spojité náhodné proměnné X.
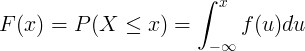
Diskrétní rozdělení
Kumulativní distribuční funkce F (x) se vypočítá součtem funkce pravděpodobnostní hmotnosti P (u) diskrétní náhodné proměnné X.

Tabulka průběžných distribucí
Kontinuální distribuce je distribuce spojité náhodné proměnné.
Příklad kontinuální distribuce
...
Tabulka průběžných distribucí
| Název distribuce | Distribuční symbol | Funkce hustoty pravděpodobnosti (pdf) | Znamenat | Rozptyl |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| Normální / gaussian | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| Jednotný | X ~ U ( a , b ) |
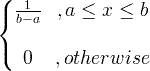 |
|
|
| Exponenciální | X ~ exp (λ) | |
|
|
| Gama | X ~ gama ( c , λ) | 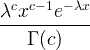 x / 0, c / 0, λ/ 0 |
|
|
| Náměstí Chi | X ~ χ 2 ( k ) |
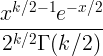 |
k |
2 k |
| Wishart | ||||
| F | X ~ F ( k 1 , k 2 ) |
|||
| Beta | ||||
| Weibulle | ||||
| Log-normální | X ~ LN (μ, σ 2 ) |
|||
| Rayleigh | ||||
| Cauchy | ||||
| Dirichlet | ||||
| Laplace | ||||
| Levy | ||||
| Rýže | ||||
| Studentská t |
Diskrétní distribuční tabulka
Diskrétní distribuce je distribuce diskrétní náhodné proměnné.
Příklad diskrétního rozdělení
...
Diskrétní distribuční tabulka
| Název distribuce | Distribuční symbol | Funkce pravděpodobnostní hmotnosti (PMF) | Znamenat | Rozptyl | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| Binomický | X ~ Bin ( n , p ) |
|
np |
np (1- p ) |
|
| jed | X ~ Poisson (λ) |
|
λ ≥ 0 |
λ |
λ |
| Jednotný | X ~ U ( a, b ) |
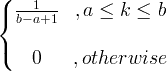 |
|
|
|
| Geometrický | X ~ Geom ( p ) |
|
|
|
|
| Hyper-geometrické | X ~ HG ( N , K , n ) |
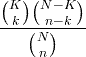 |
N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N |
|
|
| Bernoulli | X ~ Bern ( p ) |
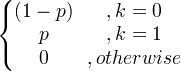 |
p |
p (1- p ) |
|
Viz také
PRAVDĚPODOBNOST A STATISTIKA
- Základní pravděpodobnost
- Očekávání
- Rozptyl
- Standardní odchylka
- Rozdělení pravděpodobnosti
- Normální distribuce
- Statistické symboly
RYCHLÉ STOLY