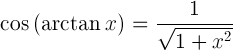Arkustangensová funkce
Arctan (x), tan -1 (x), inverzní tangenciální funkce.
Definice arktanu
Arktangenta x je definována jako inverzní tangenciální funkce x, když x je skutečné (x ∈ℝ ).
Když je tečna y rovna x:
tan y = x
Pak arkustangens x se rovná inverzní tangenciální funkci x, která se rovná y:
arctan x = tan -1 x = y
Příklad
arktan 1 = tan -1 1 = π / 4 rad = 45 °
Graf arktanu
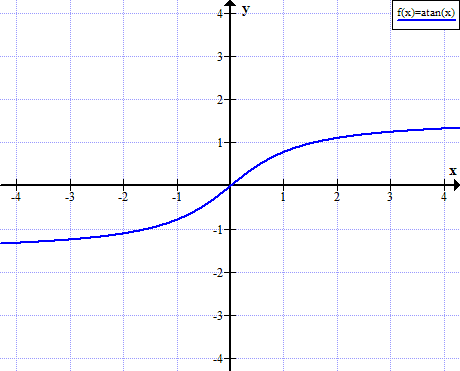
Arctan vládne
| Název pravidla | Pravidlo |
|---|---|
| Tečna arkustangensu | tan (arctan x ) = x |
| Arktan negativních argumentů | arctan (- x ) = - arctan x |
| Arktanová suma | arctan α + arctan β = arctan [( α + β ) / (1- αβ )] |
| Arktanový rozdíl | arctan α - arctan β = arctan [( α - β ) / (1+ αβ )] |
| Sinus arkustangensu | |
| Kosinus arkustangensu | |
| Reciproční argument | 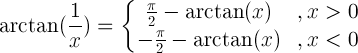 |
| Arktan z arcsinu | |
| Derivát arktanu | |
| Neurčitý integrál arktanu | |
Arktanový stůl
| x | arktan (x) (rad) |
arktan (x) (°) |
|---|---|---|
| -∞ | -π / 2 | -90 ° |
| -3 | -1,2490 | -71,565 ° |
| -2 | -1.1071 | -63,435 ° |
| -√ 3 | -π / 3 | -60 ° |
| -1 | -π / 4 | -45 ° |
| -1 / √ 3 | -π / 6 | -30 ° |
| -0,5 | -0,4636 | -26,565 ° |
| 0 | 0 | 0 ° |
| 0,5 | 0,4636 | 26,565 ° |
| 1 / √ 3 | π / 6 | 30 ° |
| 1 | π / 4 | 45 ° |
| √ 3 | π / 3 | 60 ° |
| 2 | 1.1071 | 63,435 ° |
| 3 | 1,2490 | 71,565 ° |
| ∞ | π / 2 | 90 ° |
Viz také
- Tečná funkce
- Funkce arkkosinu
- Funkce Arcsine
- Arktan z 0
- Arktan z 1
- Arktan ze 2
- Arktan nekonečna
- Derivát arktanu
- Integrace arktanu
- Sinus arktanu
- Kosinus z arktanu
- Arktanový graf
- Arktanová kalkulačka
- Převodník stupňů na radiány
TRIGONOMETRIE
RYCHLÉ STOLY