Integreret

Integration er den omvendte funktion af afledning.

Integriteten af ​​en funktion er området under funktionens graf.

Ubestemt integraldefinition

Hvornår dF (x) / dx = f (x) =/ integreret (f (x) * dx) = F (x) + c

Ubestemte integrale egenskaber

integral (f (x) + g (x)) * dx = integral (f (x) * dx) + integral (g (x) * dx)

integral (a * f (x) * dx) = a * integral (f (x) * dx)

integreret (f (a * x) * dx) = 1 / a * F (a * x) + c

integreret (f (x + b) * dx) = F (x + b) + c

integreret (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

integreret (df (x) / dx * dx) = f (x)

Ændring af integrationsvariabel

Hvornår x = g (t)  og dx = g '(t) * dt

integral (f (x) * dx) = integral (f (g (t)) * g '(t) * dt)

Integration af dele

integreret (f (x) * g '(x) * dx) = f (x) * g (x) - integreret (f' (x) * g (x) * dx)

Integraltabel

integreret (f (x) * dx = F (x) + c

integral (a * dx) = a * x + c

integreret (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, når en </ - 1

integreret (1 / x * dx) = ln (abs (x)) + c

integreret (e ^ x * dx) = e ^ x + c

integreret (a ^ x * dx) = a ^ x / ln (x) + c

integreret (ln (x) * dx) = x * ln (x) - x + c

integral (sin (x) * dx) = -cos (x) + c

integral (cos (x) * dx) = sin (x) + c

integreret (tan (x) * dx) = -ln (abs (cos (x))) + c

integreret (bueform (x) * dx) = x * bueform (x) + sqrt (1-x ^ 2) + c

integreret (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2) + c

integreret (arctan (x) * dx) = x * arctan (x) - 1/2 * ln (1 + x ^ 2) + c

integreret (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

integreret (1 / sqrt (a ^ 2-x ^ 2) * dx) = bueform (x / a) + c

integreret (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

integreret (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

integreret (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arctan (x / a) + c

integreret (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

integreret (sinh (x) * dx) = cosh (x) + c

integral (cosh (x) * dx) = sinh (x) + c

integreret (tanh (x) * dx) = ln (cosh (x)) + c

 

Definitiv integreret definition

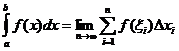
integreret (a..b, f (x) * dx) = lim (n-/ inf, sum (i = 1..n, f (z (i)) * dx (i)))  

Hvornår x0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

Definitiv integralberegning

Hvornår  ,

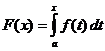  dF (x) / dx = f (x)  og

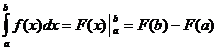
integreret (a..b, f (x) * dx) = F (b) - F (a)  

Definitive integrale egenskaber

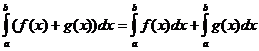
integral (a..b, (f (x) + g (x)) * dx) = integral (a..b, f (x) * dx) + integral (a..b, g (x) * dx )

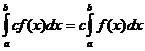
integral (a..b, c * f (x) * dx) = c * integral (a..b, f (x) * dx)

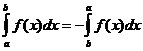
integral (a..b, f (x) * dx) = - integral (b..a, f (x) * dx)

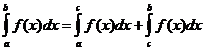
integral (a..b, f (x) * dx) = integral (a..c, f (x) * dx) + integral (c..b, f (x) * dx)

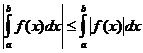
abs (integreret (a..b, f (x) * dx)) <= integral (a..b, abs (f (x)) * dx)

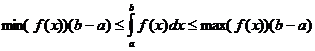min (f (x)) * (ba) <= integreret (a..b, f (x) * dx) <= max (f (x)) * (ba)  hvornår x medlem af [a, b]

Ændring af integrationsvariabel

Hvornår x = g (t)  , dx = g '(t) * dt  , g (alfa) = a  , g (beta) = b

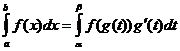
integral (a..b, f (x) * dx) = integral (alfa..beta, f (g (t)) * g '(t) * dt)

Integration af dele

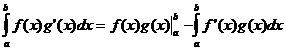
integral (a..b, f (x) * g '(x) * dx) = integral (a..b, f (x) * g (x) * dx) - integral (a..b, f' (x) * g (x) * dx)

Gennemsnitlig værdi sætning

Når f ( x ) er kontinuerlig, er der et punkt c er medlem af [a, b]  så

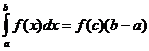
integreret (a..b, f (x) * dx) = f (c) * (ba)   

Trapesformet tilnærmelse af bestemt integral

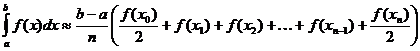
integreret (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

Gamma-funktionen

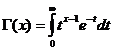
gamma (x) = integreret (0..inf, t ^ (x-1) * e ^ (- t) * dt

Gamma-funktionen er konvergent for x/ 0 .

Gamma-funktionsegenskaber

G ( x +1) = x G ( x )

G ( n +1) = n ! , når n ℕ (positivt heltal). er medlem af

Betafunktionen

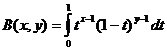
B (x, y) = integreret (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

Betafunktion og gammafunktionsrelation

B (x, y) = Gamma (x) * Gamma (y) / Gamma (x + y)

 

 

 

KALKULUS
HUKyLabsIGE TABLER