Quadratische Gleichung
Die quadratische Gleichung ist ein Polynom zweiter Ordnung mit 3 Koeffizienten - a , b , c .
Die quadratische Gleichung ist gegeben durch:
ax 2 + bx + c = 0
Die Lösung der quadratischen Gleichung ergibt sich aus 2 Zahlen x 1 und x 2 .
Wir können die quadratische Gleichung in die Form ändern:
( x - x 1 ) ( x - x 2 ) = 0
Quadratische Formel
Die Lösung der quadratischen Gleichung ergibt sich aus der quadratischen Formel:
![]()
Der Ausdruck innerhalb der Quadratwurzel wird als Diskriminante bezeichnet und mit Δ bezeichnet:
Δ = b 2 - 4 ac
Die quadratische Formel mit Diskriminanznotation:
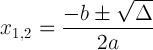
Dieser Ausdruck ist wichtig, weil er uns über die Lösung informieren kann:
- Wenn Δ/ 0 ist, gibt es 2 reelle Wurzeln x 1 = (- b + √ Δ ) / (2a) und x 2 = (- b - √ Δ ) / (2a) .
- Wenn Δ = 0 ist, gibt es eine Wurzel x 1 = x 2 = -b / (2a) .
- Wenn Δ <0 ist, gibt es keine reellen Wurzeln, es gibt 2 komplexe Wurzeln:
x 1 = (- b + i√ -Δ ) / (2a) und x 2 = (- bi√ -Δ ) / (2a) .
Problem Nr. 1
3 x 2 +5 x +2 = 0
Lösung:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Problem Nr. 2
3 x 2 -6 x +3 = 0
Lösung:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Problem Nr. 3
x 2 +2 x +5 = 0
Lösung:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16) )) / 2
Es gibt keine wirklichen Lösungen. Die Werte sind komplexe Zahlen:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Quadratischer Funktionsgraph
Die quadratische Funktion ist eine Polynomfunktion zweiter Ordnung:
f ( x ) = ax 2 + bx + c
Die Lösungen für die quadratische Gleichung sind die Wurzeln der quadratischen Funktion, dh die Schnittpunkte des quadratischen Funktionsgraphen mit der x-Achse, wenn
f ( x ) = 0
Wenn es 2 Schnittpunkte des Graphen mit der x-Achse gibt, gibt es 2 Lösungen für die quadratische Gleichung.
Wenn es 1 Schnittpunkt des Graphen mit der x-Achse gibt, gibt es 1 Lösung für die quadratische Gleichung.
Wenn es keine Schnittpunkte des Graphen mit der x-Achse gibt, erhalten wir keine realen Lösungen (oder 2 komplexe Lösungen).