Natürlicher Logarithmus - ln (x)
Natürlicher Logarithmus ist der Logarithmus zur Basis e einer Zahl.
- Definition des natürlichen Logarithmus (ln)
- Regeln und Eigenschaften des natürlichen Logarithmus (ln)
- Komplexer Logarithmus
- Graph von ln (x)
- Tabelle der natürlichen Logarithmen (ln)
- Natürlicher Logarithmusrechner
Definition des natürlichen Logarithmus
Wann
e y = x
Dann ist der Basis-e-Logarithmus von x
ln ( x ) = log e ( x ) = y
Die e-Konstante oder Eulers Zahl ist:
e ≈ 2.71828183
Ln als Umkehrfunktion der Exponentialfunktion
Die natürliche Logarithmusfunktion ln (x) ist die Umkehrfunktion der Exponentialfunktion e x .
Für x/ 0 ist
f ( f -1 ( x )) = e ln ( x ) = x
Oder
f -1 ( f ( x )) = ln ( e x ) = x
Natürliche Logarithmusregeln und Eigenschaften
| Regelname | Regel | Beispiel |
|---|---|---|
Produktregel |
ln ( x ∙ y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
Quotientenregel |
ln ( x / y ) = ln ( x ) - ln ( y ) |
ln (3 / 7) = ln (3) - ln (7) |
Potenzregel |
ln ( x y ) = y ∙ ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
In Ableitung |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
Im Integral |
∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C. | |
ln negativer Zahl |
ln ( x ) ist undefiniert, wenn x ≤ 0 ist | |
ln Null |
ln (0) ist undefiniert | |
In einem von einem |
ln (1) = 0 | |
In der Unendlichkeit |
lim ln ( x ) = ∞, wenn x → ∞ | |
| Eulers Identität | ln (-1) = i π |
Logarithmus-Produktregel
Der Logarithmus der Multiplikation von x und y ist die Summe aus Logarithmus von x und Logarithmus von y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Zum Beispiel:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Logarithmusquotientenregel
Der Logarithmus der Division von x und y ist die Differenz des Logarithmus von x und des Logarithmus von y.
log b ( x / y ) = log b ( x ) - log b ( y )
Zum Beispiel:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Logarithmus-Potenzregel
Der Logarithmus von x, der auf die Potenz von y angehoben wird, ist das y-fache des Logarithmus von x.
log b ( x y ) = y ∙ log b ( x )
Zum Beispiel:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Ableitung des natürlichen Logarithmus
Die Ableitung der natürlichen Logarithmusfunktion ist die reziproke Funktion.
Wann
f ( x ) = ln ( x )
Die Ableitung von f (x) ist:
f ' ( x ) = 1 / x
Integral des natürlichen Logarithmus
Das Integral der natürlichen Logarithmusfunktion ist gegeben durch:
Wann
f ( x ) = ln ( x )
Das Integral von f (x) ist:
∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C.
Ln von 0
Der natürliche Logarithmus von Null ist undefiniert:
ln (0) ist undefiniert
Die Grenze nahe 0 des natürlichen Logarithmus von x, wenn x gegen Null geht, ist minus unendlich:
![]()
Ln von 1
Der natürliche Logarithmus von Eins ist Null:
ln (1) = 0
Ln der Unendlichkeit
Die Grenze des natürlichen Logarithmus der Unendlichkeit, wenn x gegen unendlich geht, ist gleich unendlich:
lim ln ( x ) = ∞, wenn x → ∞
Komplexer Logarithmus
Für komplexe Zahl z:
z = re iθ = x + iy
Der komplexe Logarithmus ist (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
Graph von ln (x)
ln (x) ist nicht für reelle nicht positive Werte von x definiert:
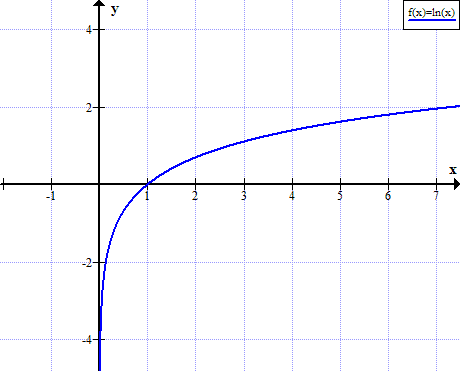
Natürliche Logarithmentabelle
| x | ln x |
|---|---|
| 0 | nicht definiert |
| 0 + | - ∞ |
| 0,0001 | -9.210340 |
| 0,001 | -6,907755 |
| 0,01 | -4.605170 |
| 0,1 | -2.302585 |
| 1 | 0 |
| 2 | 0,693147 |
| e ≈ 2,7183 | 1 |
| 3 | 1,098612 |
| 4 | 1,386294 |
| 5 | 1,609438 |
| 6 | 1,791759 |
| 7 | 1,945910 |
| 8 | 2,079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2,995732 |
| 30 | 3.401197 |
| 40 | 3,688879 |
| 50 | 3.912023 |
| 60 | 4,094345 |
| 70 | 4,248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5,703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |
Siehe auch
- Logarithmus (log)
- Natürlicher Logarithmusrechner
- Natürlicher Logarithmus von Null
- Natürlicher Logarithmus von einem
- Natürlicher Logarithmus von e
- Natürlicher Logarithmus der Unendlichkeit
- Natürlicher Logarithmus der negativen Zahl
- In umgekehrter Funktion
- In (x) Grafik
- Natürliche Logarithmentabelle
- Logarithmusrechner
- Die Konstante
ALGEBRA
SCHNELLE TABELLEN