Integral

Integration ist die umgekehrte Operation der Ableitung.

Das Integral einer Funktion ist der Bereich unter dem Funktionsgraphen.

Unbestimmte integrale Definition

Wann dF (x) / dx = f (x) =/ Integral (f (x) * dx) = F (x) + c

Unbestimmte integrale Eigenschaften

Integral (f (x) + g (x)) * dx = Integral (f (x) * dx) + Integral (g (x) * dx)

Integral (a * f (x) * dx) = a * Integral (f (x) * dx)

Integral (f (a * x) * dx) = 1 / a * F (a * x) + c

Integral (f (x + b) * dx) = F (x + b) + c

Integral (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

Integral (df (x) / dx * dx) = f (x)

Änderung der Integrationsvariablen

Wann x = g (t)  und dx = g '(t) * dt

Integral (f (x) * dx) = Integral (f (g (t)) * g '(t) * dt)

Integration in Teilstücken

Integral (f (x) * g '(x) * dx) = f (x) * g (x) - Integral (f' (x) * g (x) * dx)

Integraltabelle

Integral (f (x) * dx = F (x) + c

Integral (a * dx) = a * x + c

Integral (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, wenn a </ - 1

Integral (1 / x * dx) = ln (abs (x)) + c

Integral (e ^ x * dx) = e ^ x + c

Integral (a ^ x * dx) = a ^ x / ln (x) + c

Integral (ln (x) * dx) = x * ln (x) - x + c

Integral (sin (x) * dx) = -cos (x) + c

Integral (cos (x) * dx) = sin (x) + c

Integral (tan (x) * dx) = -ln (abs (cos (x))) + c

Integral (Arcsin (x) * dx) = x * Arcsin (x) + sqrt (1-x ^ 2) + c

Integral (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2) + c

Integral (Arctan (x) * dx) = x * Arctan (x) - 1/2 * ln (1 + x ^ 2) + c

Integral (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

Integral (1 / sqrt (a ^ 2-x ^ 2) * dx) = Arcsin (x / a) + c

Integral (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

Integral (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

Integral (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * Arctan (x / a) + c

Integral (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

Integral (sinh (x) * dx) = cosh (x) + c

Integral (cosh (x) * dx) = sinh (x) + c

Integral (tanh (x) * dx) = ln (cosh (x)) + c

 

Definitive integrale Definition

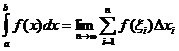
Integral (a..b, f (x) * dx) = lim (n-/ inf, Summe (i = 1..n, f (z (i)) * dx (i)))  

Wann x0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

Definitive Integralberechnung

Wann  ,

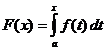  dF (x) / dx = f (x)  und

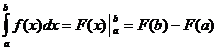
Integral (a..b, f (x) * dx) = F (b) - F (a)  

Bestimmte integrale Eigenschaften

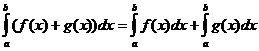
Integral (a..b, (f (x) + g (x)) * dx) = Integral (a..b, f (x) * dx) + Integral (a..b, g (x) * dx )

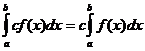
Integral (a..b, c * f (x) * dx) = c * Integral (a..b, f (x) * dx)

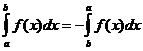
Integral (a..b, f (x) * dx) = - Integral (b..a, f (x) * dx)

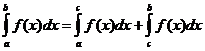
Integral (a..b, f (x) * dx) = Integral (a..c, f (x) * dx) + Integral (c..b, f (x) * dx)

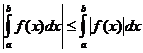
abs (Integral (a..b, f (x) * dx)) <= Integral (a..b, abs (f (x)) * dx)

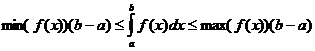min (f (x)) * (ba) <= Integral (a..b, f (x) * dx) <= max (f (x)) * (ba)  wann x Mitglied von [a, b]

Änderung der Integrationsvariablen

Wann x = g (t)  , dx = g '(t) * dt  , g (alpha) = a  , g (beta) = b

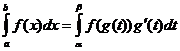
Integral (a..b, f (x) * dx) = Integral (alpha..beta, f (g (t)) * g '(t) * dt)

Integration in Teilstücken

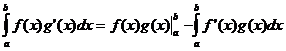
Integral (a..b, f (x) * g '(x) * dx) = Integral (a..b, f (x) * g (x) * dx) - Integral (a..b, f' (x) * g (x) * dx)

Mittelwertsatz

Wenn f ( x ) stetig ist, gibt es einen Punkt c ist Mitglied von [a, b]  damit

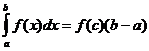
Integral (a..b, f (x) * dx) = f (c) * (ba)   

Trapezförmige Approximation eines bestimmten Integrals

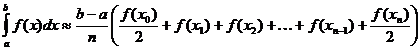
Integral (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. + f (x (n-1)) + f (x (n)) / 2)

Die Gammafunktion

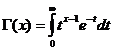
gamma (x) = Integral (0..inf, t ^ (x-1) * e ^ (- t) * dt

Die Gamma-Funktion ist konvergent für x/ 0 .

Eigenschaften der Gammafunktion

G ( x + 1) = x G ( x )

G ( n + 1) = n ! , wenn n ℕ (positive ganze Zahl). ist Mitglied von

Die Beta-Funktion

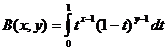
B (x, y) = Integral (0,1, t ^ (n-1) * (1-t) ^ (y-1) * dt

Beta-Funktion und Gammafunktionsbeziehung

B (x, y) = Gamma (x) · Gamma (y) / Gamma (x + y)

 

 

 

INFINITESIMALRECHNUNG
SCHNELLE TABELLEN