Περιελιγμός
Το Convolution είναι η συνάρτηση συσχέτισης του f (τ) με την αντίστροφη συνάρτηση g (t-τ).
Ο χειριστής της συνέλιξης είναι το σύμβολο αστερίσκου * .
- Συνεχής συνέλιξη
- Διακριτή συνέλιξη
- 2D διακριτή συνέλιξη
- Φιλτράρετε την εφαρμογή με συνέλιξη
- Θεώρημα της συνέλευσης
Συνεχής συνέλιξη
Η συνέλιξη των f (t) και g (t) είναι ίση με το ακέραιο των f (τ) φορές f (t-τ):
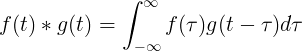
Διακριτή συνέλιξη
Η σύγκλιση 2 διακριτών συναρτήσεων ορίζεται ως:
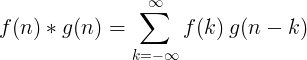
2D διακριτή συνέλιξη
Η δισδιάστατη διακριτή συνέλιξη χρησιμοποιείται συνήθως για την επεξεργασία εικόνας.
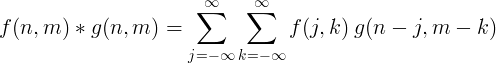
Φιλτράρετε την εφαρμογή με συνέλιξη
Μπορούμε να φιλτράρουμε το διακριτό σήμα εισόδου x (n) με συνέλιξη με την παλμική απόκριση h (n) για να πάρουμε το σήμα εξόδου y (n).
y ( n ) = x ( n ) * h ( n )
Θεώρημα της συνέλευσης
Ο μετασχηματισμός Fourier ενός πολλαπλασιασμού 2 συναρτήσεων είναι ίσος με την συνελιγμό των μετασχηματισμών Fourier κάθε λειτουργίας:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
Ο μετασχηματισμός Fourier μιας συνέλιξης 2 συναρτήσεων ισούται με τον πολλαπλασιασμό των μετασχηματισμών Fourier κάθε λειτουργίας:
F { f * g } = ℱ { f } ⋅ ℱ { g }
Θεώρημα συνέλιξης για συνεχή μετασχηματισμό Fourier
F { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
F { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
Θεώρημα συνέλιξης για διακριτό μετασχηματισμό Fourier
F { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
F { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
Θεώρημα συνέλιξης για μετασχηματισμό Laplace
F { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )
Δείτε επίσης
ΛΟΓΙΣΜΟΣ
- Οριο
- Παράγωγο
- Αναπόσπαστο
- Σειρά
- Μετασχηματισμός Laplace
- Περιελιγμός
- Λογιστικά σύμβολα
ΓΡΗΓΟΡΑ ΠΙΝΑΚΕΣ