Ruutvõrrand
Ruutvõrrand on teise astme polünoom 3 koefitsiendiga - a , b , c .
Ruutvõrrandi annab:
kirves 2 + bx + c = 0
Ruutvõrrandi lahendi annavad 2 arvu x 1 ja x 2 .
Ruutvõrrandi saame muuta järgmiseks:
( x - x 1 ) ( x - x 2 ) = 0
Ruutvormel
Ruutvõrrandi lahendi annab ruutvalem:
![]()
Ruutjuure sees olevat väljendit nimetatakse eristavaks ja tähistatakse Δ:
Δ = b 2 - 4 ac
Ruutvalem diskrimineeriva tähisega:
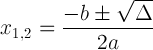
See väljend on oluline, kuna see võib meile lahenduse kohta öelda:
- Kui Δ/ 0, on 2 tegelikku juurt x 1 = (- b + √ Δ ) / (2a) ja x 2 = (- b-√ Δ ) / (2a) .
- Kui Δ = 0, on üks juur x 1 = x 2 = -b / (2a) .
- Kui Δ <0, pole tegelikke juuri, on 2 keerukat juurt:
x 1 = (- b + i√ -Δ ) / (2a) ja x 2 = (- bi√ -Δ ) / (2a) .
Probleem nr 1
3 x 2 +5 x +2 = 0
lahendus:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5-1) / 6 = -6/6 = -1
Probleem nr 2
3 x 2 -6 x +3 = 0
lahendus:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2–4 × 3 × 3)) / (2 × 3) = (6 ± √ (36–36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Probleem nr 3
x 2 +2 x +5 = 0
lahendus:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16) )) / 2
Reaalseid lahendusi pole. Väärtused on kompleksarvud:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Ruutfunktsioonide graafik
Ruutfunktsioon on teist järku polünoomfunktsioon:
f ( x ) = telg 2 + bx + c
Ruutvõrrandi lahendid on ruutfunktsiooni juured, mis on ruutfunktsioonigraafi ristumiskohad x-teljega, kui
f ( x ) = 0
Kui graafikul on x-teljega 2 lõikepunkti, on ruutvõrrandile kaks lahendit.
Kui graafiku x-teljega lõikepunkt on 1, on ruutvõrrandile 1 lahendus.
Kui graafi x-teljega lõikepunkte pole, saame mitte reaalsed lahendused (või 2 komplekslahendust).