Looduslik logaritm - ln (x)
Looduslik logaritm on arvu aluse e logaritm.
- Loodusliku logaritmi (ln) määratlus
- Loodusliku logaritmi (ln) reeglid ja omadused
- Kompleksne logaritm
- Graafik ln (x)
- Looduslike logaritmide (ln) tabel
- Loodusliku logaritmi kalkulaator
Loodusliku logaritmi määratlus
Millal
e y = x
Siis põhineb x-i logaritm
ln ( x ) = log e ( x ) = y
E pidev või Euleri arv on:
e ≈ 2,71828183
Ln eksponentsiaalfunktsiooni pöördfunktsioonina
Loodusliku logaritmi funktsioon ln (x) on eksponentsiaalfunktsiooni e x pöördfunktsioon .
Kui x/ 0,
f ( f -1 ( x )) = e ln ( x ) = x
Või
f- 1 ( f ( x )) = ln ( e x ) = x
Loodusliku logaritmi reeglid ja omadused
| Reegli nimi | Reegel | Näide |
|---|---|---|
Toote reegel |
ln ( x ∙ y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
Quotient reegel |
ln ( x / y ) = ln ( x ) - ln ( y ) |
ln (3 / 7) = ln (3) - ln (7) |
Võimu reegel |
ln ( x y ) = y ∙ ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
tuletis |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
lahutamatu |
∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C | |
Negatiivse arvu ln |
ln ( x ) on määratlemata, kui x ≤ 0 | |
ln nullist |
ln (0) pole määratletud | |
Ühest |
ln (1) = 0 | |
ln lõpmatus |
lim ln ( x ) = ∞, kui x → ∞ | |
| Euleri identiteet | ln (-1) = i π |
Logaritmi toote reegel
X ja y korrutamise logaritm on x ja y logaritmi summa.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Näiteks:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Logaritmi jagatisreegel
X ja y jagunemise logaritm on x ja y logaritmi erinevus.
log b ( x / y ) = log b ( x ) - log b ( y )
Näiteks:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Logaritmi võimsuse reegel
Y-i astmele tõstetud x-i logaritm on y-kordne x-i logaritm.
log b ( x y ) = y ∙ log b ( x )
Näiteks:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Loodusliku logaritmi tuletis
Loodusliku logaritmi funktsiooni tuletis on vastastikune funktsioon.
Millal
f ( x ) = ln ( x )
F (x) tuletis on:
f ' ( x ) = 1 / x
Loodusliku logaritmi lahutamatu osa
Loodusliku logaritmi funktsiooni integraali annab:
Millal
f ( x ) = ln ( x )
F (x) integraal on:
∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C
Ln 0-st
Nulli loomulik logaritm pole määratletud:
ln (0) pole määratletud
Kui x läheneb nullile, on naturaalse logaritmi 0 lähedal olev piir, kui x läheneb nullile, miinus lõpmatus:
![]()
Ln 1-st
Ühe looduslik logaritm on null:
ln (1) = 0
Ln lõpmatus
Lõpmatuse loodusliku logaritmi piir, kui x läheneb lõpmatusele, on võrdne lõpmatusega:
lim ln ( x ) = ∞, kui x → ∞
Kompleksne logaritm
Kompleksarvu z korral:
z = re iθ = x + iy
Kompleksne logaritm on (n = ...- 2, -1,0,1,2, ...):
Logi z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arktaan ( y / x ))
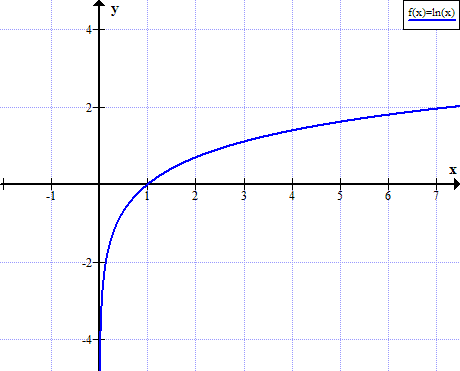
Graafik ln (x)
ln (x) ei ole määratletud x tegelike mitte-positiivsete väärtuste korral:
Looduslike logaritmide tabel
| x | ln x |
|---|---|
| 0 | määratlemata |
| 0 + | - ∞ |
| 0,0001 | -9,210340 |
| 0,001 | -6,907755 |
| 0,01 | -4,605170 |
| 0,1 | -2,302585 |
| 1 | 0 |
| 2 | 0,693147 |
| e ≈ 2,7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1,791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |
Vaata ka
- Logaritm (log)
- Loodusliku logaritmi kalkulaator
- Nulli loomulik logaritm
- Ühe loomulik logaritm
- Looduslik logaritm e
- Lõputuse loomulik logaritm
- Negatiivse arvu looduslik logaritm
- Ln pöördfunktsioon
- ln (x) graafik
- Loodusliku logaritmi tabel
- Logaritmi kalkulaator
- e konstantne
ALGEBRA
KIIRED TABELID