Pöördumine
Konvolutsioon on f (τ) korrelatsioonifunktsioon pöördfunktsiooniga g (t-τ).
Konvolutsiooni operaator on tärn sümbol * .
- Pidev pöördumine
- Diskreetne pöördumine
- 2D diskreetne pöördumine
- Filtreeri rakendus koos pöördega
- Konversiooniteoreem
Pidev pöördumine
F (t) ja g (t) konvolutsioon on võrdne f (τ) ja f (t-τ) integraaliga:
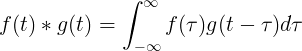
Diskreetne pöördumine
Kahe diskreetse funktsiooni teisendamine on määratletud järgmiselt:
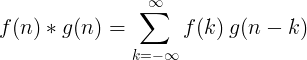
2D diskreetne pöördumine
Pilditöötluseks kasutatakse tavaliselt kahemõõtmelist diskreetset konvolutsiooni.
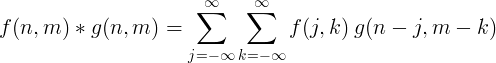
Filtreeri rakendus koos pöördega
Diskreetset sisendsignaali x (n) saame väljundsignaali y (n) saamiseks konverteerida impulssreaktsiooniga h (n).
y ( n ) = x ( n ) * h ( n )
Konversiooniteoreem
2 funktsiooni korrutise Fourieri teisendus võrdub iga funktsiooni Fourieri teisenduste konvolutsiooniga:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
2 funktsiooni konvolutsiooni Fourieri teisendus võrdub iga funktsiooni Fourieri teisenduste korrutamisega:
ℱ { f * g } = ℱ { f } ⋅ ℱ { g }
Konversiooniteoreem pideva Fourieri teisenduse jaoks
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
Konversiooniteoreem diskreetse Fourieri teisenduse jaoks
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
Konversiooniteoreem Laplace'i teisendamiseks
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )
Vaata ka
KALKULUS
- Piir
- Tuletis
- Integraalne
- Seeria
- Laplace'i teisendus
- Pöördumine
- Kalkulaatori sümbolid
KIIRED TABELID