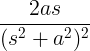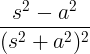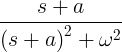Laplace'i teisendus

Laplace'i teisendus teisendab ajadomeeni funktsiooni s-domeenifunktsiooniks integreerides nullist lõpmatusse

 ajadomeeni funktsiooni korrutatuna e -st-ga .

Laplace'i teisendust kasutatakse diferentsiaalvõrrandite ja integraalide kiireks lahendamiseks.

Tulemus ajas muudetakse s-domeenis korrutamiseks s-ga.

Integreerimine ajadomeenis muudetakse s-domeenis jagunemiseks s-ga.

Laplace'i teisendusfunktsioon

Laplace'i teisendus määratakse operaatoriga L {}:

F (s) = \ mathcal {L} \ vasak \ {f (t) \ right \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt

Pööratud Laplace'i teisendus

Laplace'i pöördteisendit saab arvutada otse.

Tavaliselt antakse pöördteisendus teisenduste tabelist.

Laplace'i teisendustabel

Funktsiooni nimi Aja domeeni funktsioon Laplace'i teisendus

f ( t )

F ( s ) = L { f ( t )}
Pidev 1 \ frac {1} {s}
Lineaarne t \ frac {1} {s ^ 2}
Võimsus

t n

\ frac {n!} {s ^ {n + 1}}
Võimsus

t a

Γ ( 1) ⋅ s - ( 1)
Eksponent

e kell

\ frac {1} {sa}
Siinus

patt kell

\ frac {a} {s ^ 2 + a ^ 2}
Kosinus

cos kell

\ frac {s} {s ^ 2 + a ^ 2}
Hüperboolne siinus

sinh juures

\ frac {a} {s ^ 2-a ^ 2}
Hüperboolne koosinus

cosh kell

\ frac {s} {s ^ 2-a ^ 2}
Kasvav siinus

t sin at

\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}
Kasvav koosinus

t cos juures

\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}
Lagunev siinus

e -at sin ωt

\ frac {\ omega} {\ vasakule (s + a \ paremale) ^ 2 + \ omega ^ 2}
Lagunev koosinus

e -at cos ωt

\ frac {s + a} {\ vasakule (s + a \ paremale) ^ 2 + \ omega ^ 2}
Delta funktsioon

δ ( t )

1

Hilinenud delta

δ ( ta )

e -as

Laplace'i teisendamise omadused

Kinnistu nimi Aja domeeni funktsioon Laplace'i teisendus Kommentaar
 

f ( t )

F ( s )

  
Lineaarsus af ( t ) + bg ( t ) aF ( s ) + bG ( s ) a , b on konstantsed
Skaala muutmine f ( kell ) \ frac {1} {a} F \ vasakule (\ frac {s} {a} \ paremale) a / 0
Shift e -at f ( t ) F ( s + a )  
Viivitus f ( ta ) e - kui F ( s )  
Tuletus \ frac {df (t)} {dt} sF ( s ) - f (0)  
N-nda tuletis \ frac {d ^ nf (t)} {dt ^ n} s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0)  
Võimsus t n f ( t ) (-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}  
Integratsioon \ int_ {0} ^ {t} f (x) dx \ frac {1} {s} F  
Vastastikune \ frac {1} {t} f (t) \ int_ {s} ^ {\ infty} F (x) dx  
Pöördumine f ( t ) * g ( t ) F ( s ) ⋅ G ( s ) * on konvolutsiooni operaator
Perioodiline funktsioon f ( t ) = f ( t + T ) \ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx  

Laplace'i teisendusnäited

Näide 1

Leidke f (t) teisendus:

f ( t ) = 3 t + 2 t 2

Lahendus:

ℒ { t } = 1 / s 2

ℒ { t 2 } = 2 / s 3

F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3

 

Näide 2

Leidke F (s) pöördteisendus:

F ( s ) = 3 / ( s 2 + s - 6)

Lahendus:

Pöördtransformatsiooni leidmiseks peame s-domeeni funktsiooni muutma lihtsamaks vormiks:

F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)

[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]

a ( s +3) + b ( s -2) = 3

A ja b leidmiseks saame 2 võrrandit - ühe s-koefitsiendist ja teise ülejäänud:

( a + b ) s + 3 a -2 b = 3

a + b = 0, 3 a -2 b = 3

a = 3/5, b = -3/5

F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)

Nüüd saab F (s) teisendada hõlpsalt, kasutades eksponentfunktsiooni teisendustabelit:

f ( t ) = (3/5) e 2 t - (3/5) e -3 t

 

Vaata ka

KALKULUS
KIIRED TABELID