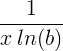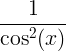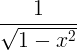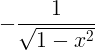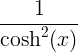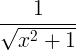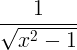Tuletisreeglid

Tuletisreeglid ja seadused. Funktsioonide tuletiste tabel.

Tuletise määratlus

Funktsiooni tuletis on funktsiooniväärtuse f (x) erinevuse suhe punktides x + Δx ja x punktiga Δx, kui Δx on lõpmata väike. Tuletis on puutuja joone funktsiooni kalle või kalle punktis x.

 

f '(x) = \ lim _ {\ Delta x \ to 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}

Teine tuletis

Teise tuletise annab:

Või tuletage lihtsalt esimene tuletis:

f

N-nda tuletis

N järku tuletis arvutatakse tuletamise f (x) n korda.

N järku tuletis võrdub tuletis (n-1) derivaat:

f ( n ) ( x ) = [ f ( n- 1) ( x )] '

Näide:

Leidke neljas tuletis

f ( x ) = 2 x 5

f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' = [40 x 3 ] '' = [120 x 2 ] '= 240 x

Tuletis funktsiooni graafikul

Funktsiooni tuletis on tangentsiaaljoone kalle.

Tuletisreeglid

Tuletatud summa reegel

( af ( x ) + bg ( x )) "= af" ( x ) + bg " ( x )
Tuletistoodete reegel

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Tuletatud jagatisreegel 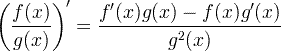\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}
Tuletisahela reegel

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Tuletatud summa reegel

Kui a ja b on konstandid.

( af ( x ) + bg ( x )) "= af" ( x ) + bg " ( x )

Näide:

Leidke tuletis:

3 x 2 + 4 x.

Summa reegli kohaselt:

a = 3, b = 4

f ( x ) = x 2 , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Tuletistoodete reegel

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Tuletatud jagatisreegel

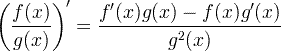
\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}

Tuletisahela reegel

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Seda reeglit saab paremini mõista Lagrange'i märkega:

\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}

Funktsiooni lineaarne lähendamine

Väikese Δx korral saame ligikaudse väärtuse f (x 0 + Δx), kui teame f (x 0 ) ja f '(x 0 ):

f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x

Funktsioonide tuletiste tabel

Funktsiooni nimi Funktsioon Tuletis

f ( x )

 f '( x )
Pidev

konst

0

Lineaarne

x

1

Võimsus

x a

kirves a- 1
Eksponentsiaalne

e x

e x
Eksponentsiaalne

a x

a x ln a
Looduslik logaritm

ln ( x )

Logaritm

log b ( x )

Siinus

patt x

cos x
Kosinus

cos x

-sin x
Tangent

tan x

Arcsine

arcsin x

Arccosine

arccos x

Arkangent

arktaan x
Hüperboolne siinus

sinh x

cosh x
Hüperboolne koosinus

cosh x

sinh x
Hüperboolne puutuja

tanh x

Pöördhüperboolne siinus

sinh -1 x

Pöördhüperboolne koosinus

cosh -1 x

Pöördhüperboolne puutuja

tanh -1 x

Tuletatud näited

Näide 1

f ( x ) = x 3 +5 x 2 + x +8

f ' ( x ) = 3 x 2 + 2 ~ 5 x + 1 + 0 = 3 x 2 +10 x +1

Näide 2

f ( x ) = patt (3 x 2 )

Ahelareegli rakendamisel tehke järgmist.

f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x

Teine tuletistest

Kui funktsiooni esimene tuletis on punktis x 0 null .

f '( x 0 ) = 0

Siis saab teine ​​tuletis punktis x 0 , f "(x 0 ), näidata selle punkti tüüpi:

 

f "( x 0 )/ 0

 kohalik miinimum

f "( x 0 ) <0

 kohalik maksimum

f "( x 0 ) = 0

 määramata

 

Vaata ka

KALKULUS
KIIRED TABELID