Neliöyhtälö
Neliöyhtälö on toisen kertaluvun polynomi, jolla on 3 kerrointa - a , b , c .
Toissijainen yhtälö saadaan:
kirves 2 + bx + c = 0
Ratkaisu toisen asteen yhtälöön annetaan kahdella luvulla x 1 ja x 2 .
Voimme muuttaa asteen yhtälön muotoon:
( x - x 1 ) ( x - x 2 ) = 0
Toissijainen kaava
Ratkaisu toisen asteen yhtälöön saadaan asteikolla:
![]()
Neliöjuuren sisällä olevaa ilmaisua kutsutaan syrjiväksi ja sitä merkitään Δ:
Δ = b 2 - 4 ac
Neliöllinen kaava erottelevalla merkinnällä:
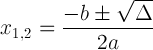
Tämä ilmaus on tärkeä, koska se voi kertoa meille ratkaisusta:
- Kun Δ/ 0, on 2 todellista juurta x 1 = (- b + √ Δ ) / (2a) ja x 2 = (- b-√ Δ ) / (2a) .
- Kun Δ = 0, on yksi juuri x 1 = x 2 = -b / (2a) .
- Kun Δ <0, ei ole todellisia juuria, on 2 kompleksista juurta:
x 1 = (- b + i√ -Δ ) / (2a) ja x 2 = (- bi√ -Δ ) / (2a) .
Ongelma # 1
3 x 2 +5 x +2 = 0
ratkaisu:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 x 3 x 2)) / (2 x 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5-1) / 6 = -6/6 = -1
Ongelma # 2
3 x 2 -6 x +3 = 0
ratkaisu:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 x 3 x 3)) / (2 x 3) = (6 ± √ (36-36)) / 6 = 6 (± 0) / 6
x 1 = x 2 = 1
Ongelma # 3
x 2 +2 x +5 = 0
ratkaisu:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16) )) / 2
Todellisia ratkaisuja ei ole. Arvot ovat kompleksilukuja:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Neliöllinen toimintakaavio
Neliöfunktio on toisen asteen polynomifunktio:
f ( x ) = akseli 2 + bx + c
Neliöyhtälön ratkaisut ovat neliöfunktion juuret, jotka ovat neliöfunktiokaavion x-akselin leikkauspisteet, kun
f ( x ) = 0
Kun kuvaajan ja x-akselin välillä on 2 leikkauspistettä, neliöyhtälölle on 2 ratkaisua.
Kun kuvaajan ja x-akselin välillä on yksi leikkauspiste, neliöyhtälöön on yksi ratkaisu.
Kun kuvaajan ja x-akselin välillä ei ole leikkauspisteitä, saamme ei todellisia ratkaisuja (tai 2 monimutkaista ratkaisua).