Luonnollinen logaritmi - ln (x)
Luonnollinen logaritmi on numeron perustan e logaritmi.
- Luonnollisen logaritmin (ln) määritelmä
- Luonnollisen logaritmin (ln) säännöt ja ominaisuudet
- Monimutkainen logaritmi
- Kuvaaja ln (x)
- Luonnollisen logaritmin (ln) taulukko
- Luonnollisen logaritmin laskin
Määritelmä luonnollinen logaritmi
Kun
e y = x
Sitten x: n e-logaritmi on
ln ( x ) = log e ( x ) = y
E vakio tai Eulerin luku on:
e ≈ 2,71828183
Ln eksponenttifunktion käänteisfunktiona
Luonnollisen logaritmin funktio ln (x) on käänteisfunktio eksponenttifunktio e x .
Jos x/ 0,
f ( f -1 ( x )) = e ln ( x ) = x
Tai
f- 1 ( f ( x )) = ln ( e x ) = x
Luonnollisen logaritmin säännöt ja ominaisuudet
| Säännön nimi | Sääntö | Esimerkki |
|---|---|---|
Tuotesääntö |
ln ( x ∙ y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
Quotient-sääntö |
ln ( x / y ) = ln ( x ) - ln ( y ) |
ln (3 / 7) = ln (3) - ln (7) |
Tehosääntö |
ln ( x y ) = y ∙ ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
johdannainen |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
olennainen osa |
∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C | |
ln negatiivista lukua |
ln ( x ) on määrittelemätön, kun x ≤ 0 | |
ln nolla |
ln (0) on määrittelemätön | |
Yksi niistä |
ln (1) = 0 | |
Loputon |
lim ln ( x ) = ∞, kun x → ∞ | |
| Eulerin henkilöllisyys | ln (-1) = i π |
Logaritmin tuotesääntö
X: n ja y: n kertologaritmi on x: n ja y: n logaritmin summa.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Esimerkiksi:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Logaritmin osamääräsääntö
X: n ja y: n jakauman logaritmi on x: n ja y: n logaritmin ero.
log b ( x / y ) = log b ( x ) - log b ( y )
Esimerkiksi:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Logaritmin tehosääntö
Y: n voimaksi korotetun x: n logaritmi on y kertaa x: n logaritmi.
log b ( x y ) = y ∙ log b ( x )
Esimerkiksi:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Luonnollisen logaritmin johdannainen
Luonnollisen logaritmifunktion derivaatti on vastavuoroinen funktio.
Kun
f ( x ) = ln ( x )
F (x): n johdannainen on:
f ' ( x ) = 1 / x
Luonnollisen logaritmin integraali
Luonnollisen logaritmin funktion integraali saadaan:
Kun
f ( x ) = ln ( x )
F (x): n integraali on:
∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C
Ln 0: sta
Nollan luonnollinen logaritmi on määrittelemätön:
ln (0) on määrittelemätön
Raja lähellä x: n luonnollisen logaritmin arvoa 0, kun x lähestyy nollaa, on miinus ääretön:
![]()
Ln yhdestä
Yhden luonnollinen logaritmi on nolla:
ln (1) = 0
Ln ääretön
Äärettömyyden luonnollisen logaritmin raja, kun x lähestyy ääretöntä, on yhtä suuri kuin ääretön:
lim ln ( x ) = ∞, kun x → ∞
Monimutkainen logaritmi
Kompleksiluvulle z:
z = re iθ = x + iy
Kompleksinen logaritmi on (n = ...- 2, -1,0,1,2, ...):
Loki z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
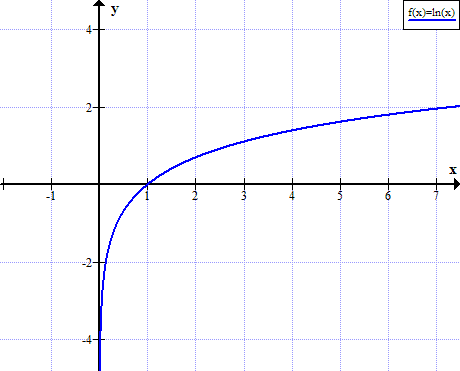
Kuvaaja ln (x)
ln (x) ei ole määritelty x: n todellisille ei-positiivisille arvoille:
Luonnollisen logaritmin taulukko
| x | ln x |
|---|---|
| 0 | undefined |
| 0 + | - ∞ |
| 0,0001 | -9,210340 |
| 0,001 | -6,907755 |
| 0,01 | -4,605170 |
| 0,1 | -2,302585 |
| 1 | 0 |
| 2 | 0,693147 |
| e ≈ 2,7183 | 1 |
| 3 | 1.098612 |
| 4 | 1,386294 |
| 5 | 1,609438 |
| 6 | 1,791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4,248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6,214608 |
| 600 | 6.396930 |
| 700 | 6,551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |
Katso myös
- Logaritmi (loki)
- Luonnollisen logaritmin laskin
- Luonnollinen logaritmi nollasta
- Yhden luonnollinen logaritmi
- Luonnollinen logaritmi e
- Infiniitin luonnollinen logaritmi
- Negatiivisen luvun luonnollinen logaritmi
- Ln käänteisfunktio
- ln (x) kaavio
- Luonnollisen logaritmin taulukko
- Logaritmin laskin
- e vakio
ALGEBRA
NOPEAT PÖYTÄT