Intégral

L'intégration est l'opération inverse de la dérivation.

L'intégrale d'une fonction est la zone sous le graphique de la fonction.

Définition intégrale indéfinie

Quand dF (x) / dx = f (x) =/ intégrale (f (x) * dx) = F (x) + c

Propriétés intégrales indéfinies

intégrale (f (x) + g (x)) * dx = intégrale (f (x) * dx) + intégrale (g (x) * dx)

intégrale (a * f (x) * dx) = a * intégrale (f (x) * dx)

intégrale (f (a * x) * dx) = 1 / a * F (a * x) + c

intégrale (f (x + b) * dx) = F (x + b) + c

intégrale (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

intégrale (df (x) / dx * dx) = f (x)

Changement de variable d'intégration

Quandx = g (t) etdx = g '(t) * dt

intégrale (f (x) * dx) = intégrale (f (g (t)) * g '(t) * dt)

Intégration par pièces

intégrale (f (x) * g '(x) * dx) = f (x) * g (x) - intégrale (f' (x) * g (x) * dx)

Table des intégrales

intégrale (f (x) * dx = F (x) + c

intégrale (a * dx) = a * x + c

intégrale (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, quand a </ - 1

intégrale (1 / x * dx) = ln (abs (x)) + c

intégrale (e ^ x * dx) = e ^ x + c

intégrale (a ^ x * dx) = a ^ x / ln (x) + c

intégrale (ln (x) * dx) = x * ln (x) - x + c

intégrale (sin (x) * dx) = -cos (x) + c

intégrale (cos (x) * dx) = sin (x) + c

intégrale (tan (x) * dx) = -ln (abs (cos (x))) + c

intégrale (arcsin (x) * dx) = x * arcsin (x) + sqrt (1-x ^ 2) + c

intégrale (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2) + c

intégrale (arctan (x) * dx) = x * arctan (x) - 1/2 * ln (1 + x ^ 2) + c

intégrale (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

intégrale (1 / sqrt (a ^ 2-x ^ 2) * dx) = arcsin (x / a) + c

intégrale (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

intégrale (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

intégrale (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arctan (x / a) + c

intégrale (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

intégrale (sinh (x) * dx) = cosh (x) + c

intégrale (cosh (x) * dx) = sinh (x) + c

intégrale (tanh (x) * dx) = ln (cosh (x)) + c

 

Définition intégrale définie

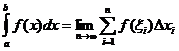
intégrale (a..b, f (x) * dx) = lim (n-/ inf, somme (i = 1..n, f (z (i)) * dx (i))) 

Quandx0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

Calcul intégral défini

Quand ,

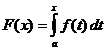 dF (x) / dx = f (x) et

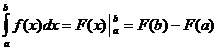
intégrale (a..b, f (x) * dx) = F (b) - F (a) 

Propriétés intégrales définies

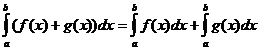
intégrale (a..b, (f (x) + g (x)) * dx) = intégrale (a..b, f (x) * dx) + intégrale (a..b, g (x) * dx )

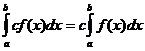
intégrale (a..b, c * f (x) * dx) = c * intégrale (a..b, f (x) * dx)

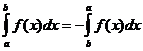
intégrale (a..b, f (x) * dx) = - intégrale (b..a, f (x) * dx)

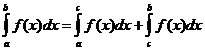
intégrale (a..b, f (x) * dx) = intégrale (a..c, f (x) * dx) + intégrale (c..b, f (x) * dx)

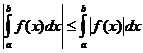
abs (intégrale (a..b, f (x) * dx)) <= intégrale (a..b, abs (f (x)) * dx)

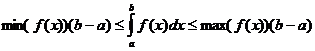min (f (x)) * (ba) <= intégrale (a..b, f (x) * dx) <= max (f (x)) * (ba) quandx membre de [a, b]

Changement de variable d'intégration

Quandx = g (t) ,dx = g '(t) * dt ,g (alpha) = a ,g (bêta) = b

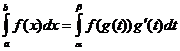
intégrale (a..b, f (x) * dx) = intégrale (alpha..beta, f (g (t)) * g '(t) * dt)

Intégration par pièces

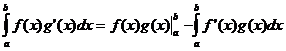
intégrale (a..b, f (x) * g '(x) * dx) = intégrale (a..b, f (x) * g (x) * dx) - intégrale (a..b, f' (x) * g (x) * dx)

Théorème de la valeur moyenne

Quand f ( x ) est continue il y a un pointc est membre de [a, b] donc

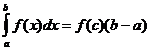
intégrale (a..b, f (x) * dx) = f (c) * (ba)  

Approximation trapézoïdale de l'intégrale définie

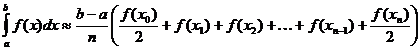
intégrale (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

La fonction gamma

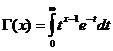
gamma (x) = intégrale (0..inf, t ^ (x-1) * e ^ (- t) * dt

La fonction Gamma est convergente pour x/ 0 .

Propriétés de la fonction gamma

G ( x +1) = x G ( x )

G ( n +1) = n ! , quand n ℕ (entier positif).est membre de

La fonction bêta

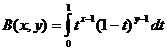
B (x, y) = intégrale (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

Relation entre la fonction bêta et la fonction gamma

B (x, y) = Gamma (x) * Gamma (y) / Gamma (x + y)

 

 

 

CALCUL
TABLES RAPIDES