Fonction Arcsine
arcsin (x), sin -1 (x), fonction sinusoïdale inverse .
Définition de l'arcsin
L'arc sinus de x est défini comme la fonction sinusoïdale inverse de x lorsque -1≤x≤1.
Lorsque le sinus de y est égal à x:
sin y = x
Alors l'arc sinus de x est égal à la fonction sinus inverse de x, qui est égale à y:
arcsin x = sin -1 x = y
Exemple
arcsin 1 = sin -1 1 = π / 2 rad = 90 °
Graphique d'arcsin
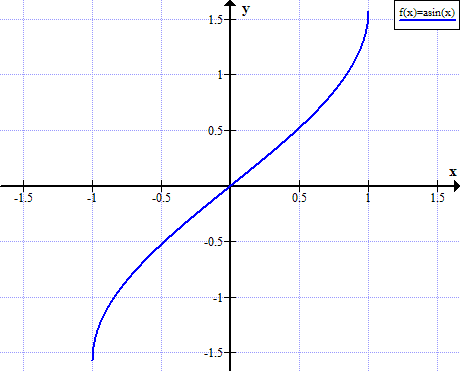
Règles d'Arcsin
| Nom de la règle | Règle |
|---|---|
| Sinus de l'arc sinus | sin (arcsin x ) = x |
| Arc sinusoïdal | arcsin (sin x ) = x +2 k π, quand k ∈ℤ ( k est un entier) |
| Arcsin d'argument négatif | arcsin (- x ) = - arcsin x |
| Angles complémentaires | arcsin x = π / 2 - arccos x = 90 ° - arccos x |
| Arcsin somme | arcsine α + arcsine ( β ) = arcsine ( α√ (1- β 2 ) + β√ (1- α 2 ) ) |
| Différence Arcsin | arcsine α - arcsine ( β ) = arcsine ( α√ (1- β 2 ) - β√ (1- α 2 ) ) |
| Cosinus de l'arc sinus | |
| Tangente de l'arc sinus | |
| Dérivée de l'arc sinus | 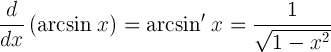 |
| Intégrale indéfinie de l'arc sinus |
Table Arcsin
| x | arcsin (x) (rad) |
arcsin (x) (°) |
|---|---|---|
| -1 | -π / 2 | -90 ° |
| -√ trois / deux | -π / 3 | -60 ° |
| -√ 2 /2 | -π / 4 | -45 ° |
| -1/2 | -π / 6 | -30 ° |
| 0 | 0 | 0 ° |
| 1/2 | π / 6 | 30 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ trois / 2 | π / 3 | 60 ° |
| 1 | π / 2 | 90 ° |
Voir également
- Fonction sinus
- Fonction Arccosine
- Fonction Arctan
- Calculatrice Arcsin
- Convertisseur de degrés en radians
- Arcsin de 0
- Arcsin de 1
- Arcsin de l'infini
- Graphique Arcsin
- Dérivé d'Arcsin
- Intégrale d'Arcsin
- Péché d'Arcsin
- Cos d'Arcsin
- Tan d'Arcsin