કન્વોલ્યુશન
કન્વોલ્યુશન એ વિપરીત ફંક્શન જી (ટી-τ) સાથે એફ (τ) નું સહસંબંધ કાર્ય છે.
કન્વોલ્યુશન operatorપરેટર એસ્ટરિસ્ક સિમ્બોલ છે * .
સતત સંકલ્પ
એફ (ટી) અને જી (ટી) નું કન્વોલ્યુશન એફ (τ) ટાઇમ એફ (ટી-τ) ના અવિભાજ્ય સમાન છે:
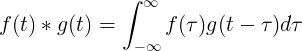
સ્વતંત્ર સંકલ્પ
2 સ્વતંત્ર કાર્યોના કન્વોલ્યુશનને આ પ્રમાણે વ્યાખ્યાયિત કરવામાં આવે છે:
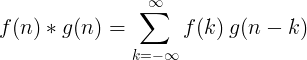
2 ડી સ્વતંત્ર સમાધાન
સામાન્ય રીતે ઇમેજ પ્રોસેસિંગ માટે 2 પરિમાણીય ડિસ્રેટ કન્વોલ્યુશનનો ઉપયોગ થાય છે.
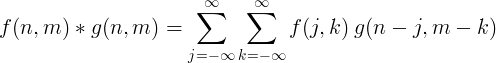
દ્રષ્ટિ સાથે ફિલ્ટર અમલીકરણ
આઉટપુટ સિગ્નલ y (n) મેળવવા માટે આપણે ઇમ્પલ્સ રિસ્પોન્સ h (n) સાથે દિવાલો દ્વારા ડિસ્રિક્ટ ઇનપુટ સિગ્નલ x (n) ને ફિલ્ટર કરી શકીએ છીએ.
y ( n ) = x ( n ) * h ( n )
કન્વોલ્યુશન પ્રમેય
2 ફંક્શનના ગુણાકારનું ફ્યુરીઅર ટ્રાન્સફોર્મ દરેક ફંક્શનના ફ્યુરિયર ટ્રાન્સફોર્મ્સના સમાધાન સમાન છે:
ℱ { એફ ⋅ ગ્રામ } = ℱ { એફ } * ℱ { ગ્રામ }
2 કાર્યોના મંતવ્યનું ફ્યુરિયર ટ્રાન્સફોર્મ દરેક ફંક્શનના ફ્યુરિયર ટ્રાન્સફોર્મ્સના ગુણાકાર જેટલું છે:
ℱ { એફ * ગ્રામ } = ℱ { એફ } ⋅ ℱ { ગ્રામ }
સતત ફ્યુરિયર ટ્રાન્સફોર્મ માટે કન્વોલ્યુશન પ્રમેય
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
સ્વતંત્ર ફ્યુરિયર ટ્રાન્સફોર્મ માટે કન્વોલ્યુશન પ્રમેય
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n ) F = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n ) F = F ( k ) ⋅ G ( k )
લેપ્લેસ ટ્રાન્સફોર્મ માટે કન્વોલ્યુશન પ્રમેય
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )
આ પણ જુઓ
કેલ્ક્યુલસ
- મર્યાદા
- વ્યુત્પન્ન
- અભિન્ન
- શ્રેણી
- લેપલેસ રૂપાંતર
- કન્વોલ્યુશન
- કેલ્ક્યુલસ પ્રતીકો
ઝડપી ટેબલ્સ