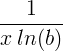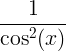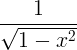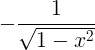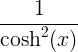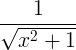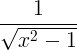વ્યુત્પન્ન નિયમો
વ્યુત્પન્ન નિયમો અને કાયદા. કાર્યો કોષ્ટકના વ્યુત્પત્તિઓ.
વ્યુત્પન્ન વ્યાખ્યા
ફંક્શનનું વ્યુત્પન્ન એ બિંદુઓ x + Δx અને x સાથે valuex, જ્યારે Δx અનંતરૂપે નાના હોય ત્યારે ફંક્શન મૂલ્ય એફ (એક્સ) ના તફાવતનું ગુણોત્તર છે. ડેરિવેટિવ એ બિંદુ x પર સ્પર્શ વાક્યનું કાર્ય opeાળ અથવા opeાળ છે.
![]()
બીજું વ્યુત્પન્ન
બીજું ડેરિવેટિવ આ દ્વારા આપવામાં આવ્યું છે:
![]()
અથવા ફક્ત પ્રથમ વ્યુત્પન્ન પ્રાપ્ત કરો:
![]()
નવમી વ્યુત્પન્ન
એ મી વ્યુત્પન્ન f (x) એ વખત બન્યું દ્વારા ગણવામાં આવે છે.
એ મી વ્યુત્પન્ન છે (N-1) વ્યુત્પન્ન વ્યુત્પન્ન માટે સમાન:
f ( n ) ( x ) = [ f ( n -1) ( x )] '
ઉદાહરણ:
નું ચોથું વ્યુત્પન્ન શોધો
f ( x ) = 2 x 5
f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x
ફંક્શનના ગ્રાફ પર વ્યુત્પન્ન
ફંક્શનનું વ્યુત્પન્ન કરનાર એ સ્પર્શીય રેખાની .ાળ છે.
વ્યુત્પન્ન નિયમો
| વ્યુત્પન્ન રકમનો નિયમ | ( એએફ ( એક્સ ) + BG ( એક્સ )) '= એએફ' ( એક્સ ) + BG ' ( એક્સ ) |
| વ્યુત્પન્ન ઉત્પાદનનો નિયમ | ( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| વ્યુત્પન્ન ગુણાંક નિયમ | 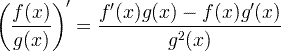 |
| વ્યુત્પન્ન સાંકળ નિયમ | f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
વ્યુત્પન્ન રકમનો નિયમ
જ્યારે એ અને બી સ્થિર હોય છે.
( એએફ ( એક્સ ) + BG ( એક્સ )) '= એએફ' ( એક્સ ) + BG ' ( એક્સ )
ઉદાહરણ:
નું વ્યુત્પન્ન શોધો:
3 x 2 + 4 x.
સરવાળો નિયમ મુજબ:
a = 3, b = 4
f ( x ) = x 2 , g ( x ) = x
f ' ( x ) = 2 x , g' ( x ) = 1
(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4
વ્યુત્પન્ન ઉત્પાદનનો નિયમ
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
વ્યુત્પન્ન ગુણાંક નિયમ
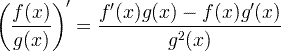
વ્યુત્પન્ન સાંકળ નિયમ
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
આ નિયમ લેગ્રેંજની નોંધ સાથે વધુ સારી રીતે સમજી શકાય છે:
![]()
કાર્ય રેખીય આશરે
નાના Δx માટે, આપણે f (x 0 + Δx) ની નજીકનો વિચાર કરી શકીએ છીએ, જ્યારે આપણે f (x 0 ) અને f '(x 0 ) ને જાણીએ છીએ :
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x
કાર્યો કોષ્ટકના વ્યુત્પત્તિઓ
| કાર્ય નામ | કાર્ય | વ્યુત્પન્ન |
|---|---|---|
| f ( x ) |
f '( x ) | |
| સતત | કોન્સ્ટ |
0 |
| રેખીય | x |
1 |
| પાવર | x એ |
કુહાડી એ- 1 |
| ઘાતાંકીય | e x |
e x |
| ઘાતાંકીય | એક એક્સ |
a x ln a |
| કુદરતી લોગરીધમ | એલએન ( એક્સ ) |
|
| લોગરીધમ | લોગ બી ( એક્સ ) |
|
| સાઇન | sin x |
કોસ એક્સ |
| કોઝિન | કોસ એક્સ |
-સિન એક્સ |
| ટેન્જેન્ટ | ટેન એક્સ |
|
| આર્ક્સિન | આર્ક્સિન એક્સ |
|
| આર્કોઝિન | આર્કોકોસ એક્સ |
|
| આર્કટેન્જેન્ટ | આર્કટન x |
|
| હાયપરબોલિક સાઇન | સિન્હ એક્સ |
કોશ એક્સ |
| હાયપરબોલિક કોસાઇન | કોશ એક્સ |
સિન્હ એક્સ |
| હાયપરબોલિક સ્પર્શ | તન્હ એક્સ |
|
| Inંધી હાયપરબોલિક સાઇન | sinh -1 x |
|
| વ્યસ્ત હાયપરબોલિક કોસાઇન | કોશ -1 x |
|
| Verseંધી હાયપરબોલિક સ્પર્શ | તન્હ -1 x |
|
વ્યુત્પન્ન ઉદાહરણો
ઉદાહરણ # 1
f ( x ) = x 3 +5 x 2 + x +8
f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
ઉદાહરણ # 2
f ( x ) = sin (3 x 2 )
સાંકળ નિયમ લાગુ કરતી વખતે:
f ' ( x ) = કોસ (3 x 2 ) ⋅ [3 x 2 ]' = કોસ (3 x 2 ) ⋅ 6 x
બીજી વ્યુત્પન્ન કસોટી
જ્યારે ફંકશનનું પ્રથમ વ્યુત્પન્ન બિંદુ x 0 પર શૂન્ય છે .
f '( x 0 ) = 0
પછી બિંદુ x 0 , f '' (x 0 ) પરનું બીજું વ્યુત્પન્ન , તે બિંદુનો પ્રકાર સૂચવી શકે છે:
| f '' ( x 0 )/ 0 |
સ્થાનિક લઘુત્તમ |
| f '' ( x 0 ) <0 |
સ્થાનિક મહત્તમ |
| f '' ( x 0 ) = 0 |
અનિશ્ચિત |
આ પણ જુઓ
કેલ્ક્યુલસ
- મર્યાદા
- વ્યુત્પન્ન
- અભિન્ન
- શ્રેણી
- લેપલેસ રૂપાંતર
- કન્વોલ્યુશન
- કેલ્ક્યુલસ પ્રતીકો
ઝડપી ટેબલ્સ