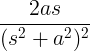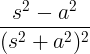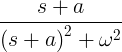લેપલેસ ટ્રાન્સફોર્મ
લapપ્લેસ શૂન્યથી અનંતમાં સંકલન દ્વારા ટાઇમ ડોમેન ફંક્શનને એસ-ડોમેન ફંક્શનમાં રૂપાંતરિત કરે છે
સમય ડોમેન ફંક્શનનું, ઇ -st દ્વારા ગુણાકાર .
લેપલેસ ટ્રાન્સફોર્મનો ઉપયોગ વિભેદક સમીકરણો અને ઇન્ટિગ્રેલ્સ માટે ઝડપથી ઉકેલો શોધવા માટે થાય છે.
સમય ડોમેનમાં વ્યુત્પત્તિ એસ-ડોમેનમાંના ગુણાકારમાં રૂપાંતરિત થાય છે.
સમય ડોમેનમાં એકીકરણ s દ્વારા ડોમેન દ્વારા વિભાજનમાં રૂપાંતરિત થાય છે.
લેપલેસ ટ્રાન્સફોર્મ ફંક્શન
લ apપ્લેસ ટ્રાન્સફોર્મ એલ {} ઓપરેટર સાથે વ્યાખ્યાયિત થયેલ છે :
![]()
Inંધી લapપલેસ રૂપાંતર
Inંધી લapપ્લેસ ટ્રાન્સફોર્મની સીધી ગણતરી કરી શકાય છે.
સામાન્ય રીતે પરિવર્તન કોષ્ટકમાંથી verseંધી પરિવર્તન આપવામાં આવે છે.
લેપ્લેસ ટ્રાન્સફોર્મ ટેબલ
| કાર્ય નામ | સમય ડોમેન કાર્ય | લેપલેસ રૂપાંતર |
|---|---|---|
એફ ( ટી ) |
F ( s ) = L { f ( t ) |
|
| સતત | 1 | |
| રેખીય | ટી | |
| પાવર | ટી એન |
|
| પાવર | ટી એ |
Γ ( a +1) ⋅ s - ( a +1) |
| ઘાતક | ઇ અંતે |
|
| સાઇન | પાપ પર |
|
| કોઝિન | કોસ પર |
|
| હાયપરબોલિક સાઇન | sinh અંતે |
|
| હાયપરબોલિક કોસાઇન | અંતે કોશ |
|
| સાઇન વધતી | ટી પાપ પર |
|
| વધતી કોસિન | ટી કોસ પર |
|
| ક્ષીણ સાઇન | e -at પાપ ωt |
|
| ક્ષીણ થઈ રહેલા કોસાઇન | e -at કોસ ωt |
|
| ડેલ્ટા ફંક્શન | t ( ટી ) |
1 |
| વિલંબિત ડેલ્ટા | ta ( તા ) |
e -as |
લેપલેસ પરિવર્તન ગુણધર્મો
| મિલકત નામ | સમય ડોમેન કાર્ય | લેપલેસ રૂપાંતર | ટિપ્પણી |
|---|---|---|---|
એફ ( ટી ) |
F ( ઓ ) |
||
| રેખીયતા | એએફ ( T ) + BG ( T ) | એએફ ( ઓ ) + બીજી ( ઓ ) | એ , બી સ્થિર છે |
| સ્કેલ ફેરફાર | એફ ( અંતે ) | |
a / 0 |
| પાળી | e -at f ( t ) | F ( s + a ) | |
| વિલંબ | એફ ( તા ) | ઈ - કારણ કે એફ ( ઓ ) | |
| વ્યુત્પત્તિ | |
એસએફ ( ઓ ) - એફ (0) | |
| N-th વ્યુત્પન્ન | |
s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0) | |
| પાવર | ટી એન એફ ( ટી ) | |
|
| એકીકરણ | |
|
|
| પારસ્પરિક | |
|
|
| કન્વોલ્યુશન | f ( t ) * g ( t ) | એફ ( ઓ ) ⋅ જી ( ઓ ) | * કન્વોલ્યુશન operatorપરેટર છે |
| સામયિક કાર્ય | f ( t ) = f ( t + T ) | |
લેપ્લેસ ઉદાહરણો બદલી
ઉદાહરણ # 1
એફ (ટી) નું પરિવર્તન શોધો:
f ( t ) = 3 ટી + 2 ટી 2
ઉકેલો:
ℒ { t } = 1 / s 2
ℒ { t 2 } = 2 / s 3
F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3
ઉદાહરણ # 2
એફ (ઓ) નું વ્યસ્ત પરિવર્તન શોધો:
એફ ( ઓ ) = 3 / ( સે 2 + સે - 6)
ઉકેલો:
Verseંધી પરિવર્તન શોધવા માટે, અમારે ડોમેન કાર્યને એક સરળ સ્વરૂપમાં બદલવાની જરૂર છે:
F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)
[ a ( s +3) + બી ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]
a ( s +3) + b ( s -2) = 3
A અને b શોધવા માટે, અમને 2 સમીકરણો મળે છે - એકના સહગુણાંકોમાંથી એક અને બાકીનું બીજું:
( a + b ) s + 3 a -2 b = 3
a + b = 0, 3 a -2 b = 3
a = 3/5, બી = -3/5
F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)
હવે એફ (ઓ) ને ઘાતક કાર્ય માટે ટ્રાન્સફોર્મ ટેબલનો ઉપયોગ કરીને સરળતાથી બદલી શકાય છે:
f ( t ) = (3/5) e 2 t - (3/5) e -3 t
આ પણ જુઓ
કેલ્ક્યુલસ
- મર્યાદા
- વ્યુત્પન્ન
- અભિન્ન
- શ્રેણી
- લેપલેસ રૂપાંતર
- કન્વોલ્યુશન
- કેલ્ક્યુલસ પ્રતીકો
ઝડપી ટેબલ્સ