משוואה ריבועית
משוואה ריבועית היא פולינום מסדר שני עם 3 מקדמים - a , b , c .
המשוואה הריבועית ניתנת על ידי:
גרזן 2 + bx + c = 0
הפתרון למשוואה הריבועית ניתן על ידי 2 מספרים x 1 ו- x 2 .
אנו יכולים לשנות את המשוואה הריבועית לצורה של:
( x - x 1 ) ( x - x 2 ) = 0
נוסחה ריבועית
הפתרון למשוואה הריבועית ניתן על ידי הנוסחה הריבועית:
![]()
הביטוי בתוך השורש הריבועי נקרא מפלה ומסומן על ידי Δ:
Δ = b 2 - 4 ac
הנוסחה הריבועית עם סימון מפלה:
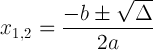
ביטוי זה חשוב מכיוון שהוא יכול לספר לנו על הפיתרון:
- כאשר Δ/ 0, ישנם 2 שורשים אמיתיים x 1 = (- b + √ Δ ) / (2a) ו- x 2 = (- b-√ Δ ) / (2a) .
- כאשר Δ = 0, יש שורש אחד x 1 = x 2 = -b / (2a) .
- כאשר Δ <0, אין שורשים אמיתיים, ישנם 2 שורשים מורכבים:
x 1 = (- b + i√ -Δ ) / (2a) ו- x 2 = (- bi√ -Δ ) / (2a) .
בעיה מס '1
3 x 2 +5 x +2 = 0
פִּתָרוֹן:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
בעיה מס '2
3 x 2 -6 x +3 = 0
פִּתָרוֹן:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
בעיה מס '3
x 2 +2 x +5 = 0
פִּתָרוֹן:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
אין פתרונות אמיתיים. הערכים הם מספרים מורכבים:
x 1 = -1 + 2 אני
x 2 = -1 - 2 אני
גרף פונקציות ריבועיות
הפונקציה הריבועית היא פונקציה פולינומית מסדר שני:
f ( x ) = גרזן 2 + bx + c
הפתרונות למשוואה הריבועית הם שורשי הפונקציה הריבועית, שהם נקודות החיתוך של גרף הפונקציות הריבועיות עם ציר ה- x, כאשר
f ( x ) = 0
כשיש שתי נקודות חיתוך של הגרף עם ציר ה- x, ישנם 2 פתרונות למשוואה הריבועית.
כשיש נקודת חיתוך אחת של הגרף עם ציר ה- x, יש פתרון אחד למשוואה הריבועית.
כשאין נקודות חיתוך של הגרף עם ציר ה- x, אנו לא מקבלים פתרונות אמיתיים (או 2 פתרונות מורכבים).