כללי לוגריתם

הבסיס ב הלוגריתם של מספר הוא המעריך כי אנחנו צריכים להעלות את הבסיס על מנת לקבל את המספר.

הגדרת לוגריתם

כאשר b מורם לעוצמה של y שווה x:

b y = x

ואז לוגריתם הבסיס של x שווה ל- y:

יומן b ( x ) = y

לדוגמא מתי:

2 4 = 16

לאחר מכן

יומן 2 (16) = 4

לוגריתם כפונקציה הפוכה של פונקציה מעריכית

הפונקציה הלוגריתמית,

y = יומן b ( x )

היא הפונקציה ההפוכה של הפונקציה האקספוננציאלית,

x = b y

אז אם נחשב את הפונקציה האקספוננציאלית של הלוגריתם של x (x/ 0),

f ( f -1 ( x )) = b log b ( x ) = x

או אם נחשב את הלוגריתם של הפונקציה האקספוננציאלית של x,

f -1 ( f ( x )) = יומן b ( b x ) = x

לוגריתם טבעי (ln)

לוגריתם טבעי הוא לוגריתם לבסיס e:

ln ( x ) = יומן e ( x )

כאשר e קבוע הוא המספר:

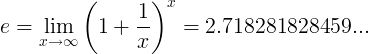
e = \ lim_ {x \ rightarrow \ infty} \ left (1+ \ frac {1} {x} \ right) ^ x = 2.718281828459 ...

או

e = \ lim_ {x \ rightarrow 0} \ left (1+ \ right x) ^ \ frac {1} {x}

 

ראה: לוגריתם טבעי

חישוב לוגריתם הפוך

הלוגריתם ההפוך (או אנטי לוגריתם) מחושב על ידי העלאת הבסיס b ללוגריתם y:

x = log -1 ( y ) = b y

פונקציה לוגריתמית

לפונקציה הלוגריתמית יש צורה בסיסית של:

f ( x ) = יומן b ( x )

חוקי הלוגריתם

שם החוק כְּלָל
כלל מוצר לוגריתם
 יומן b ( x ∙ y ) = יומן b ( x ) + יומן b ( y )
כלל מכסת לוגריתם
 יומן b ( x / y ) = יומן b ( x ) - יומן b ( y )
כלל כוח לוגריתם
 יומן b ( x y ) = y ∙ יומן b ( x )
כלל מתג בסיס לוגריתם
 יומן ב ( ג ) = 1 / יומן ג ( ב )
כלל שינוי בסיס לוגריתם
 יומן b ( x ) = יומן c ( x ) / יומן c ( ב )
נגזרת של לוגריתם
 f ( x ) = יומן b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b ))
אינטגרל של לוגריתם
 ∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
לוגריתם של המספר השלילי
 יומן b ( x ) אינו מוגדר כאשר x ≤ 0
לוגריתם של 0
 יומן b (0) אינו מוגדר
\ lim_ {x \ ל- 0 ^ +} \ textup {log} _b (x) = - \ infty
לוגריתם של 1
 יומן b (1) = 0
לוגריתם של הבסיס
 יומן ב ( ב ) = 1
לוגריתם של אינסוף
 lim log b ( x ) = ∞, כאשר x → ∞

ראה: כללי לוגריתם

 

כלל מוצר לוגריתם

הלוגריתם של הכפל של x ו- y הוא סכום הלוגריתם של x ולוגריתם של y.

יומן b ( x ∙ y ) = יומן b ( x ) + יומן b ( y )

לדוגמה:

יומן 10 (3 ∙ 7) = יומן 10 (3) + יומן 10 (7)

כלל מכסת לוגריתם

הלוגריתם של החלוקה של x ו- y הוא ההבדל של הלוגריתם של x והלוגריתם של y.

יומן b ( x / y ) = יומן b ( x ) - יומן b ( y )

לדוגמה:

יומן 10 (3 / 7) = log 10 (3) - יומן 10 (7)

כלל כוח לוגריתם

הלוגריתם של x המועלה לכוחו של y הוא y כפול הלוגריתם של x.

יומן b ( x y ) = y ∙ יומן b ( x )

לדוגמה:

יומן 10 (2 8 ) = 8 ∙ יומן 10 (2)

כלל מתג בסיס לוגריתם

לוגריתם הבסיס של c הוא 1 חלקי בסיס הלוגריתם c של b.

יומן ב ( ג ) = 1 / יומן ג ( ב )

לדוגמה:

יומן 2 (8) = 1 / יומן 8 (2)

כלל שינוי בסיס לוגריתם

בסיס לוגריתם b של x הוא לוגריתם בסיס c של x חלקי בסיס לוגריתם c של b.

יומן b ( x ) = יומן c ( x ) / יומן c ( ב )

לדוגמא, כדי לחשב את יומן 2 (8) במחשבון, עלינו לשנות את הבסיס ל -10:

יומן 2 (8) = יומן 10 (8) / יומן 10 (2)

ראה: כלל שינוי בסיס יומן הרישום

לוגריתם של המספר השלילי

הבסיס b לוגריתם אמיתי של x כאשר x <= 0 אינו מוגדר כאשר x הוא שלילי או שווה לאפס:

יומן b ( x ) אינו מוגדר כאשר x ≤ 0

ראה: יומן המספר השלילי

לוגריתם של 0

לוגריתם הבסיס b של אפס אינו מוגדר:

יומן b (0) אינו מוגדר

הגבול של לוגריתם הבסיס של x, כאשר x מתקרב לאפס, הוא מינוס אינסוף:

\ lim_ {x \ ל- 0 ^ +} \ textup {log} _b (x) = - \ infty

ראה: יומן אפס

לוגריתם של 1

הלוגריתם הבסיסי של אחד הוא אפס:

יומן b (1) = 0

לדוגמה, בסיס שני לוגריתם של אחד הוא אפס:

יומן 2 (1) = 0

ראה: יומן של אחד

לוגריתם של אינסוף

הגבול של לוגריתם הבסיס של x, כאשר x מתקרב לאינסוף, שווה לאינסוף:

lim log b ( x ) = ∞, כאשר x → ∞

ראה: יומן האינסוף

לוגריתם של הבסיס

הלוגריתם הבסיסי של b הוא אחד:

יומן ב ( ב ) = 1

לדוגמה, שני הלוגריתם הבסיסי של שניים הוא אחד:

יומן 2 (2) = 1

נגזרת לוגריתם

מתי

f ( x ) = יומן b ( x )

ואז הנגזרת של f (x):

f ' ( x ) = 1 / ( x ln ( b ))

ראה: נגזרת יומן

אינטגרל לוגריתם

אינטגרל הלוגריתם של x:

∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C

לדוגמה:

∫ יומן 2 ( x ) dx = x ∙ (יומן 2 ( x ) - 1 / ln (2) ) + C

קירוב לוגריתם

יומן 2 ( x ) ≈ n + ( x / 2 n - 1),

לוגריתם מורכב

למספר מורכב z:

z = re iθ = x + iy

הלוגריתם המורכב יהיה (n = ...- 2, -1,0,1,2, ...):

יומן z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · ארקטאן ( y / x ))

בעיות ותשובות בלוגריתם

בעיה מס '1

מצא x עבור

יומן 2 ( x ) + יומן 2 ( x -3) = 2

פִּתָרוֹן:

שימוש בכלל המוצר:

יומן 2 ( x ∙ ( x -3)) = 2

שינוי צורת הלוגריתם על פי הגדרת הלוגריתם:

x ∙ ( x -3) = 2 2

או

x 2 -3 x -4 = 0

פתרון המשוואה הריבועית:

x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1

מכיוון שהלוגריתם אינו מוגדר למספרים שליליים, התשובה היא:

x = 4

בעיה מס '2

מצא x עבור

יומן 3 ( x +2) - יומן 3 ( x ) = 2

פִּתָרוֹן:

באמצעות כלל המנה:

יומן 3 (( x +2) / x ) = 2

שינוי צורת הלוגריתם על פי הגדרת הלוגריתם:

( x +2) / x = 3 2

או

x +2 = 9 x

או

8 x = 2

או

x = 0.25

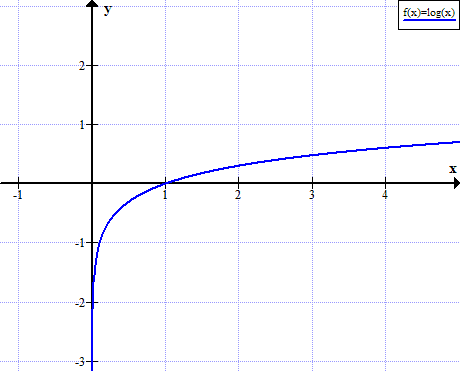
גרף יומן (x)

log (x) אינו מוגדר לערכים אמיתיים שאינם חיוביים של x:

טבלת לוגריתמים

x יומן 10 x יומן 2 x יומן e x
0 לא מוגדר לא מוגדר לא מוגדר
0 + - ∞ - ∞ - ∞
0.0001 -4 -13.287712 -9.210340
0.001 -3 -9.965784 -6.907755
0.01 -2 -6.643856 -4.605170
0.1 -1 -3.321928 -2.302585
1 0 0 0
2 0.301030 1 0.693147
3 0.477121 1.584963 1.098612
4 0.602060 2 1.386294
5 0.698970 2.321928 1.609438
6 0.778151 2.584963 1.791759
7 0.845098 2.807355 1.945910
8 0.903090 3 2.079442
9 0.954243 3.169925 2.197225
10 1 3.321928 2.302585
20 1.301030 4.321928 2.995732
30 1.477121 4.906891 3.401197
40 1.602060 5.321928 3.688879
50 1.698970 5.643856 3.912023
60 1.778151 5.906991 4.094345
70 1.845098 6.129283 4.248495
80 1.903090 6.321928 4.382027
90 1.954243 6.491853 4.499810
100 2 6.643856 4.605170
200 2.301030 7.643856 5.298317
300 2.477121 8.228819 5.703782
400 2.602060 8.643856 5.991465
500 2.698970 8.965784 6.214608
600 2.778151 9.228819 6.396930
700 2.845098 9.451211 6.551080
800 2.903090 9.643856 6.684612
900 2.954243 9.813781 6.802395
1000 3 9.965784 6.907755
10000 4 13.287712 9.210340

 

מחשבון לוגריתם ►

 

ראה גם

אַלגֶבּרָה
שולחנות מהירים