לוגריתם טבעי - ln (x)
לוגריתם טבעי הוא הלוגריתם לבסיס e של מספר.
- הגדרת לוגריתם טבעית (ln)
- כללים ותכונות של לוגריתם טבעי (ln)
- לוגריתם מורכב
- גרף של ln (x)
- טבלת לוגריתמים טבעיים (ln)
- מחשבון לוגריתם טבעי
הגדרת לוגריתם טבעי
מתי
e y = x
ואז בסיס הלוגריתם e של x הוא
ln ( x ) = log e ( x ) = y
מתמיד הדואר או מספר אוילר הוא:
ה ≈ 2.71828183
Ln כפונקציה הפוכה של פונקציה מעריכית
פונקציית הלוגריתם הטבעית ln (x) היא הפונקציה ההפוכה של הפונקציה האקספוננציאלית e x .
עבור x/ 0,
f ( f -1 ( x )) = e ln ( x ) = x
או
f -1 ( f ( x )) = ln ( e x ) = x
כללים ותכונות טבעיות של לוגריתם
| שם החוק | כְּלָל | דוגמא |
|---|---|---|
חוק מוצר |
ln ( x ∙ y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
שלטון רב |
ln ( x / y ) = ln ( x ) - ln ( y ) |
LN (3 / 7) = ln (3) - ln (7) |
שלטון כוח |
ln ( x y ) = y ∙ ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
נגזרת |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
אינטגרלי |
∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C. | |
מספר המספר השלילי |
ln ( x ) אינו מוגדר כאשר x ≤ 0 | |
בין אפס |
ln (0) אינו מוגדר | |
אחד אחד |
ln (1) = 0 | |
באינסוף |
lim ln ( x ) = ∞, כאשר x → ∞ | |
| זהות אוילר | ln (-1) = i π |
כלל מוצר לוגריתם
הלוגריתם של הכפל של x ו- y הוא סכום הלוגריתם של x ולוגריתם של y.
יומן b ( x ∙ y ) = יומן b ( x ) + יומן b ( y )
לדוגמה:
יומן 10 (3 ∙ 7) = יומן 10 (3) + יומן 10 (7)
כלל מכסת לוגריתם
הלוגריתם של החלוקה של x ו- y הוא ההבדל של הלוגריתם של x והלוגריתם של y.
יומן b ( x / y ) = יומן b ( x ) - יומן b ( y )
לדוגמה:
יומן 10 (3 / 7) = log 10 (3) - יומן 10 (7)
כלל כוח לוגריתם
הלוגריתם של x המועלה לכוחו של y הוא y כפול הלוגריתם של x.
יומן b ( x y ) = y ∙ יומן b ( x )
לדוגמה:
יומן 10 (2 8 ) = 8 ∙ יומן 10 (2)
נגזרת של לוגריתם טבעי
הנגזרת של פונקציית הלוגריתם הטבעית היא הפונקציה ההדדית.
מתי
f ( x ) = ln ( x )
הנגזרת של f (x) היא:
f ' ( x ) = 1 / x
אינטגרל של לוגריתם טבעי
האינטגרל של פונקציית הלוגריתם הטבעית ניתן על ידי:
מתי
f ( x ) = ln ( x )
האינטגרל של f (x) הוא:
∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C
Ln של 0
הלוגריתם הטבעי של אפס אינו מוגדר:
ln (0) אינו מוגדר
הגבול ליד 0 ללוגריתם הטבעי של x, כאשר x מתקרב לאפס, הוא מינוס אינסוף:
![]()
Ln של 1
הלוגריתם הטבעי של אחד הוא אפס:
ln (1) = 0
Ln של אינסוף
גבול הלוגריתם הטבעי של האינסוף, כאשר x מתקרב לאינסוף שווה לאינסוף:
lim ln ( x ) = ∞, כאשר x → ∞
לוגריתם מורכב
למספר מורכב z:
z = re iθ = x + iy
הלוגריתם המורכב יהיה (n = ...- 2, -1,0,1,2, ...):
יומן z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · ארקטאן ( y / x ))
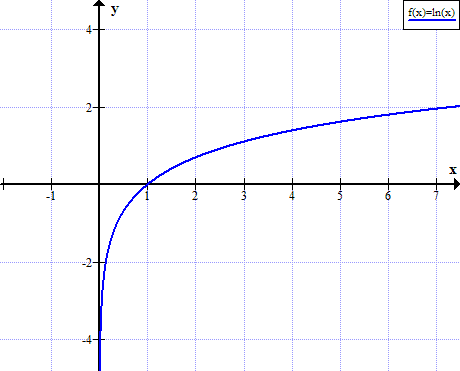
גרף של ln (x)
ln (x) אינו מוגדר לערכים אמיתיים שאינם חיוביים של x:
טבלת לוגריתמים טבעית
| x | ב x |
|---|---|
| 0 | לא מוגדר |
| 0 + | - ∞ |
| 0.0001 | -9.210340 |
| 0.001 | -6.907755 |
| 0.01 | -4.605170 |
| 0.1 | -2.302585 |
| 1 | 0 |
| 2 | 0.693147 |
| e ≈ 2.7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1.791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |
ראה גם
- לוגריתם (יומן)
- מחשבון לוגריתם טבעי
- לוגריתם טבעי של אפס
- לוגריתם טבעי של אחד
- לוגריתם טבעי של ה
- לוגריתם טבעי של אינסוף
- לוגריתם טבעי של מספר שלילי
- פונקציה הפוכה
- גרף ln (x)
- שולחן לוגריתם טבעי
- מחשבון לוגריתם
- קבוע
אַלגֶבּרָה
שולחנות מהירים