בלתי נפרד

אינטגרציה היא הפעולה ההפוכה של הגזירה.

האינטגרל של פונקציה הוא האזור שמתחת לגרף הפונקציה.

הגדרה אינטגרלית בלתי מוגבלת

מתי dF (x) / dx = f (x) =/ אינטגרלי (f (x) * dx) = F (x) + c

מאפיינים אינטגרליים בלתי מוגדרים

אינטגרל (f (x) + g (x)) * dx = אינטגרל (f (x) * dx) + אינטגרל (g (x) * dx)

אינטגרל (a * f (x) * dx) = a * אינטגרל (f (x) * dx)

אינטגרל (f (a * x) * dx) = 1 / a * F (a * x) + c

אינטגרל (f (x + b) * dx) = F (x + b) + c

אינטגרל (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

אינטגרל (df (x) / dx * dx) = f (x)

משתנה של שינוי אינטגרציה

מתי x = g (t)  ו dx = g '(t) * dt

אינטגרל (f (x) * dx) = אינטגרל (f (g (t)) * g '(t) * dt)

שילוב לפי חלקים

אינטגרל (f (x) * g '(x) * dx) = f (x) * g (x) - אינטגרלי (f' (x) * g (x) * dx)

טבלת אינטגרלים

אינטגרל (f (x) * dx = F (x) + c

אינטגרל (a * dx) = a * x + c

אינטגרל (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, כאשר </ - 1

אינטגרל (1 / x * dx) = ln (abs (x)) + c

אינטגרל (e ^ x * dx) = e ^ x + c

אינטגרל (a ^ x * dx) = a ^ x / ln (x) + c

אינטגרל (ln (x) * dx) = x * ln (x) - x + c

אינטגרל (sin (x) * dx) = -cos (x) + c

אינטגרל (cos (x) * dx) = sin (x) + c

אינטגרל (tan (x) * dx) = -ln (abs (cos (x))) + c

אינטגרלי (arcsin (x) * dx) = x * arcsin (x) + sqrt (1-x ^ 2) + c

אינטגרל (ארקוס (x) * dx) = x * ארקוס (x) - sqrt (1-x ^ 2) + c

אינטגרל (arctan (x) * dx) = x * arctan (x) - 1/2 * ln (1 + x ^ 2) + c

אינטגרל (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

אינטגרל (1 / sqrt (a ^ 2-x ^ 2) * dx) = קשת (x / a) + c

אינטגרל (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

אינטגרל (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

אינטגרל (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arctan (x / a) + c

אינטגרל (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

אינטגרל (sinh (x) * dx) = cosh (x) + c

אינטגרל (cosh (x) * dx) = sinh (x) + c

אינטגרל (tanh (x) * dx) = ln (cosh (x)) + c

 

הגדרה אינטגרלית מוגדרת

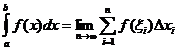
אינטגרל (a..b, f (x) * dx) = lim (n-/ inf, sum (i = 1..n, f (z (i)) * dx (i)))  

מתי x0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

חישוב אינטגרלי מובהק

מתי  ,

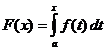  dF (x) / dx = f (x)  ו

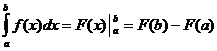
אינטגרל (a..b, f (x) * dx) = F (b) - F (a)  

מאפיינים אינטגרליים מוגדרים

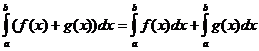
אינטגרל (a..b, (f (x) + g (x)) * dx) = אינטגרל (a..b, f (x) * dx) + אינטגרל (a..b, g (x) * dx )

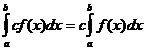
אינטגרל (a..b, c * f (x) * dx) = c * integral (a..b, f (x) * dx)

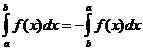
אינטגרל (a..b, f (x) * dx) = - אינטגרלי (b..a, f (x) * dx)

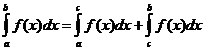
אינטגרל (a..b, f (x) * dx) = אינטגרל (a..c, f (x) * dx) + אינטגרל (c..b, f (x) * dx)

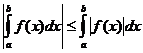
שרירי הבטן (אינטגרל (a..b, f (x) * dx)) <= אינטגרל (a..b, abs (f (x)) * dx)

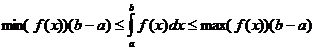min (f (x)) * (ba) <= integral (a..b, f (x) * dx) <= max (f (x)) * (ba)  מתי חבר ב- [a, b]

משתנה של שינוי אינטגרציה

מתי x = g (t)  , dx = g '(t) * dt  , g (אלפא) = א  , g (בטא) = ב

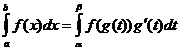
אינטגרל (a..b, f (x) * dx) = אינטגרל (alpha..beta, f (g (t)) * g '(t) * dt)

שילוב לפי חלקים

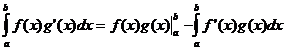
אינטגרל (a..b, f (x) * g '(x) * dx) = אינטגרל (a..b, f (x) * g (x) * dx) - אינטגרלי (a..b, f' (x) * g (x) * dx)

משפט ערך ממוצע

כאשר f ( x ) רציף יש נקודה c הוא חבר ב- [a, b]  לכן

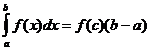
אינטגרל (a..b, f (x) * dx) = f (c) * (ba)   

קירוב טרפז של אינטגרל מוגדר

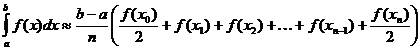
אינטגרל (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

פונקציית הגמא

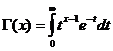
גמא (x) = אינטגרלי (0..inf, t ^ (x-1) * e ^ (- t) * dt

פונקציית הגמא מתכנסת ל- x/ 0 .

מאפייני פונקצית גמא

G ( x +1) = x G ( x )

G ( n +1) = n ! , כאשר n ℕ (מספר שלם חיובי). הוא חבר ב

פונקציית בטא

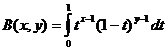
B (x, y) = נפרד (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

פונקציית בטא וקשר לתפקוד גמא

B (x, y) = גמא (x) * גמא (y) / גמא (x + y)

 

 

 

חֶשְׁבּוֹן
שולחנות מהירים