द्विघात समीकरण
द्विघात समीकरण 3 गुणांक के साथ एक दूसरा क्रम बहुपद है - ए , बी , सी ।
द्विघात समीकरण द्वारा दिया गया है:
ax 2 + bx + c = 0
द्विघात समीकरण का समाधान 2 संख्या x 1 और x 2 द्वारा दिया गया है ।
हम द्विघात समीकरण को इस रूप में बदल सकते हैं:
( x - x 1 ) ( x - x 2 ) = 0
द्विघात सूत्र
द्विघात समीकरण का समाधान द्विघात सूत्र द्वारा दिया गया है:
![]()
वर्गमूल के अंदर की अभिव्यक्ति को विभेदक कहा जाता है और इसे by द्वारा दर्शाया जाता है:
Δ = बी 2 - 4 एसी
भेदभावपूर्ण संकेतन के साथ द्विघात सूत्र:
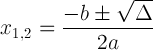
यह अभिव्यक्ति महत्वपूर्ण है क्योंकि यह हमें समाधान के बारे में बता सकती है:
- जब When/ 0, 2 वास्तविक जड़ें हैं x 1 = (- b + Δ /) / (2a) और x 2 = (- b-√ Δ ) / (2a) ।
- जब When = 0, एक रूट x 1 = x 2 = -b / (2a) होता है ।
- जब there <0, कोई वास्तविक जड़ें नहीं हैं, तो 2 जटिल जड़ें हैं:
x 1 = (- b + i√- 2 ) / (2a) और x 2 = (- bi√ -Δ ) / (2a) ।
समस्या # 1
3 x 2 +5 x +2 = 0
समाधान:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 -5 -5 (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
समस्या # 2
3 x 2 -6 x +3 = 0
समाधान:
a = 3, b = -6, c = 3
x 1,2 = (6 √ √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 √ √ (36-36)) / 6 = (6) 0) / 6
x 1 = x 2 = 1
समस्या # 3
x 2 +2 x +5 = 0
समाधान:
a = 1, b = 2, c = 5
x 1,2 = (-2 √ √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 (-2 (4-20)) / 2 = (-2 ± -2 (-16) )) / 2
कोई वास्तविक समाधान नहीं हैं। मान जटिल संख्याएँ हैं:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
द्विघात फंक्शन ग्राफ
द्विघात कार्य एक दूसरा क्रम बहुपद है:
f ( x ) = ax 2 + bx + c
द्विघात समीकरण के समाधान द्विघात फ़ंक्शन की जड़ें हैं, जो x- अक्ष के साथ द्विघात फ़ंक्शन ग्राफ के प्रतिच्छेदन बिंदु हैं, जब
f ( x ) = 0
जब एक्स-अक्ष के साथ ग्राफ के 2 चौराहे बिंदु होते हैं, तो द्विघात समीकरण के 2 समाधान होते हैं।
जब एक्स-अक्ष के साथ ग्राफ का 1 चौराहा बिंदु होता है, तो द्विघात समीकरण का 1 समाधान होता है।
जब एक्स-अक्ष के साथ ग्राफ के कोई चौराहे बिंदु नहीं होते हैं, तो हमें वास्तविक समाधान (या 2 जटिल समाधान) नहीं मिलते हैं।