लघुगणक नियम

आधार ख लघुगणक एक नंबर का है प्रतिपादक है कि हम जुटाने की जरूरत आधार आदेश संख्या प्राप्त करने के लिए।

लघुगणक परिभाषा

जब b को y की शक्ति पर उठाया जाता है तो बराबर x होता है:

बी वाई = एक्स

तब x का आधार b लघुगणक y के बराबर है:

log b ( x ) = y

उदाहरण के लिए जब:

२ ४ = १६

फिर

लॉग 2 (16) = 4

क्षणिक कार्य के व्युत्क्रम फलन के रूप में लघुगणक

लघुगणक समारोह,

y = लॉग बी ( x )

घातीय फलन का व्युत्क्रम फलन है,

x = b y

तो अगर हम x के लघुगणक (एक्स/ 0) के घातीय कार्य की गणना करते हैं,

f ( f -1 ( x )) = b log b ( x ) = x

या अगर हम एक्स के घातीय फ़ंक्शन के लघुगणक की गणना करते हैं,

f -1 ( f ( x )) = log b ( b x ) = x

प्राकृतिक लघुगणक (ln)

प्राकृतिक लघुगणक आधार के लिए एक लघुगणक है:

ln ( x ) = log e ( x )

जब ई स्थिर संख्या है:

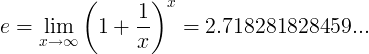
e = \ lim_ {x \ rightarrow \ infty} \ left (1+ \ frac {1} {x} \ right) ^ x = 2.718281828459 ...

या

e = \ lim_ {x \ rightarrow 0} \ बाएँ (1+ \ दाएँ x) ^ \ frac {1} {}}

 

देखें: प्राकृतिक लघुगणक

उलटा लघुगणक गणना

उलटा लघुगणक (या विरोधी लघुगणक) की गणना ख आधार को लघुगणक y से बढ़ाकर की जाती है:

x = log -1 ( y ) = b y

लघुगणक समारोह

लघुगणक समारोह का मूल रूप है:

f ( x ) = लॉग बी ( x )

लघुगणक नियम

नियम का नाम नियम
लघुगणक उत्पाद नियम
 लॉग बी ( x ) y ) = लॉग बी ( x ) + लॉग बी ( y )
लघुगणक भागफल नियम
 लॉग बी ( एक्स / वाई ) = लॉग बी ( एक्स ) - लॉग बी ( वाई )
लघुगणक शक्ति नियम
 log b ( x y ) = y b log b ( x )
लघुगणक आधार स्विच नियम
 लॉग बी ( सी ) = 1 / लॉग सी ( बी )
लघुगणक आधार परिवर्तन नियम
 लॉग बी ( एक्स ) = लॉग सी ( एक्स ) / लॉग सी ( बी )
लघुगणक के व्युत्पन्न
 f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b ))
लघुगणक का अभिन्न अंग
 ∫ लॉग बी ( एक्स ) डीएक्स = एक्स log (लॉग बी ( एक्स ) - १ / एलएन ( बी ) ) + सी
ऋणात्मक संख्या का लघुगणक
 x। 0 होने पर लॉग बी ( x ) अपरिभाषित होता है
लघुगणक ०
 लॉग बी (0) अपरिभाषित है
\ lim_ {x \ _ 0 ^ +} \ textup {log} _b (x) = - \ infty
1 का लघुगणक
 log b (1) = 0
आधार का लघुगणक
 log b ( b ) = 1
अनंत का लघुगणक
 lim log b ( x ) =) , जब x →)

देखें: लघुगणक नियम

 

लघुगणक उत्पाद नियम

X और y के गुणन का लघुगणक x के लघुगणक और y के लघुगणक का योग है।

लॉग बी ( x ) y ) = लॉग बी ( x ) + लॉग बी ( y )

उदाहरण के लिए:

लोग इन 10 (3 ∙ 7) = लोग इन 10 (3) + लोग इन 10 (7)

लघुगणक भागफल नियम

X और y के विभाजन का लघुगणक x के लघुगणक और y के लघुगणक का अंतर है।

लॉग बी ( एक्स / वाई ) = लॉग बी ( एक्स ) - लॉग बी ( वाई )

उदाहरण के लिए:

लोग इन 10 (3 / 7) = लोग इन 10 (3) - लॉग इन करें 10 (7)

लघुगणक शक्ति नियम

X का लघुगणक y की शक्ति से उठाया गया x का लघुगणक है।

log b ( x y ) = y b log b ( x )

उदाहरण के लिए:

लॉग इन करने के 10 (2 8 ) = 8 ∙ लोग इन 10 (2)

लघुगणक आधार स्विच नियम

C का आधार b लघुगणक b के आधार c लघुगणक से 1 विभाजित है।

लॉग बी ( सी ) = 1 / लॉग सी ( बी )

उदाहरण के लिए:

लॉग 2 (8) = 1 / लॉग 8 (2)

लघुगणक आधार परिवर्तन नियम

X का आधार b लघुगणक x का आधार c लघुगणक है जो b के आधारभूत लघुगणक द्वारा विभाजित है।

लॉग बी ( एक्स ) = लॉग सी ( एक्स ) / लॉग सी ( बी )

उदाहरण के लिए, कैलकुलेटर में लॉग 2 (8) की गणना करने के लिए, हमें आधार को 10 में बदलने की आवश्यकता है:

लॉग 2 (8) = लॉग 10 (8) / लॉग 10 (2)

देखें: लॉग बेस परिवर्तन नियम

ऋणात्मक संख्या का लघुगणक

जब x <= 0 अपरिभाषित हो तो x का वास्तविक लघुगणक आधार शून्य है या शून्य के बराबर है:

x। 0 होने पर लॉग बी ( x ) अपरिभाषित होता है

देखें: ऋणात्मक संख्या का लॉग

लघुगणक ०

शून्य का आधार b लघुगणक अपरिभाषित है:

लॉग बी (0) अपरिभाषित है

X के आधार b लघुगणक की सीमा, जब x शून्य के निकट आता है, माइनस इन्फिनिटी है:

\ lim_ {x \ _ 0 ^ +} \ textup {log} _b (x) = - \ infty

देखें: शून्य का लॉग

1 का लघुगणक

एक का आधार b लघुगणक शून्य है:

log b (1) = 0

उदाहरण के लिए, एक का आधार दो लघुगणक शून्य है:

log 2 (1) = 0

देखें: एक का लॉग

अनंत का लघुगणक

X के आधार b लघुगणक की सीमा, जब x अनंत तक पहुंचता है, अनंत के बराबर होता है:

lim log b ( x ) =), जब x →)

देखें: अनंत का लॉग

आधार का लघुगणक

आधार b का लघुगणक एक है:

log b ( b ) = 1

उदाहरण के लिए, आधार दो का लघुगणक एक है:

log 2 (2) = 1

लघुगणक व्युत्पन्न

कब

f ( x ) = लॉग बी ( x )

फिर च के व्युत्पन्न (एक्स):

f ' ( x ) = 1 / ( x ln ( b ))

देखें: लॉग व्युत्पन्न

लघुगणक अभिन्न

एक्स के लघुगणक का अभिन्न अंग:

∫ लॉग बी ( एक्स ) डीएक्स = एक्स log (लॉग बी ( एक्स ) - १ / एलएन ( बी ) ) + सी

उदाहरण के लिए:

∫ लॉग 2 ( x ) dx = x log (लॉग 2 ( x ) - १ / ln (२) ) + C

लघुगणक सन्निकटन

लॉग 2 ( x ) + n + ( x / 2 n - 1),

जटिल लघुगणक

जटिल संख्या z के लिए:

z = re iθ = x + iy

जटिल लघुगणक होगा (n = ... -2, -1,0,1,2, ...):

Log z = ln ( r ) + i ( 2 + 2n = ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))

लघुगणक समस्याओं और जवाब

समस्या # 1

के लिए x का पता लगाएं

log 2 ( x ) + log 2 ( x -3) = 2

समाधान:

उत्पाद नियम का उपयोग करना:

लॉग इन करें 2 ( एक्स ∙ ( एक्स -3)) = 2

लघुगणक परिभाषा के अनुसार लघुगणक रूप बदलना:

x x ( x -3) = 2 2

या

x 2 -3 x -4 = 0

द्विघात समीकरण को हल करना:

x 1,2 = [3 √ 3 ​​(9 + 16)] / 2 = [3] 5] / 2 = 4 -1 -1

चूंकि लघुगणक को ऋणात्मक संख्याओं के लिए परिभाषित नहीं किया गया है, इसलिए उत्तर है:

x = 4

समस्या # 2

के लिए x का पता लगाएं

log 3 ( x +2) - log 3 ( x ) = 2

समाधान:

भागफल नियम का उपयोग करना:

लॉग 3 (( x +2) / x ) = 2

लघुगणक परिभाषा के अनुसार लघुगणक रूप बदलना:

( x +2) / x = 3 2

या

x +2 = 9 x

या

8 x = 2

या

x = 0.25

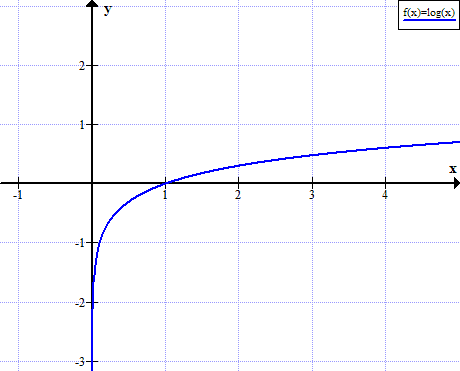
लॉग का ग्राफ (x)

लॉग (x) x के वास्तविक गैर सकारात्मक मूल्यों के लिए परिभाषित नहीं किया गया है:

लघुगणक तालिका

x लॉग 10 x लॉग 2 x लॉग ई एक्स
0 अपरिभाषित अपरिभाषित अपरिभाषित
0 + - ∞ - ∞ - ∞
0.0001 -4 -१३.२,८७,७१२ -९.२,१०,३४०
0.001 -3 -९.९,६५,७८४ -६.९,०७,७५५
0.01 -2 -६.६,४३,८५६ -४.६,०५,१७०
0.1 -1 -३.३,२१,९२८ -२.३,०२,५८५
1 0 0 0
2 0.301030 1 0.693147
3 0.477121 1.584963 1.098612
4 0.602060 2 1.386294
5 0.698970 2.321928 1.609438
6 0.778151 2.584963 1.791759
7 0.845098 2.807355 1.945910
8 0.903090 3 2.079442
9 0.954243 3.169925 2.197225
10 1 3.321928 2.302585
20 1.301030 4.321928 2.995732
30 1.477121 4.906891 3.401197
40 1.602060 5.321928 3.688879
50 1.698970 5.643856 3.912023
60 1.778151 5.906991 4.094345
70 1.845098 6.129283 4.248495
80 1.903090 6.321928 4.382027
90 1.954243 6.491853 4.499810
100 2 6.643856 4.605170
200 2.301030 7.643856 5.298317
300 2.477121 8.228819 5.703782
400 2.602060 8.643856 5.991465
500 2.698970 8.965784 6.214608
600 2.778151 9.228819 6.396930
700 2.845098 9.451211 6.551080
800 2.903090 9.643856 6.684612
900 2.954243 9.813781 6.802395
1000 3 9.965784 6.907755
10000 4 13.287712 9.210340

 

लघुगणक कैलकुलेटर ►

 

यह सभी देखें

बीजगणित
रैपिड टाइलें