कनवल्शन
कन्वर्सेशन एफ (with) का उलटा फ़ंक्शन जी (t-τ) के साथ सहसंबंध समारोह है।
दृढ़ संकल्प ऑपरेटर तारांकन चिह्न है * ।
निरंतर दृढ़ संकल्प
F (t) और g (t) का अभिप्रेरन f (τ) टाइम्स f (t-t) के अभिन्न के बराबर है:
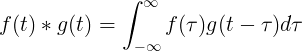
असतत आक्षेप
2 असतत कार्यों का समाधान निम्नानुसार परिभाषित किया गया है:
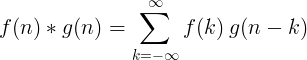
2 डी असतत सजा
2 आयामी असतत दृढ़ संकल्प आमतौर पर छवि प्रसंस्करण के लिए उपयोग किया जाता है।
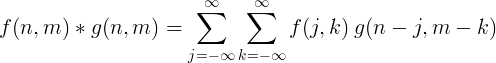
निश्चय के साथ फ़िल्टर कार्यान्वयन
हम आउटपुट सिग्नल y (n) प्राप्त करने के लिए आवेग प्रतिक्रिया h (n) के साथ कनवल्शन द्वारा असतत इनपुट सिग्नल x (n) को फ़िल्टर कर सकते हैं।
y ( n ) = x ( n ) * h ( n )
बातचीत प्रमेय
2 कार्यों के गुणन का फूरियर रूपांतरण प्रत्येक फ़ंक्शन के फूरियर रूपांतरणों के दृढ़ संकल्प के बराबर होता है:
⋅ { f } g } = ℱ { f } * g { g }
2 फ़ंक्शन के एक कन्वर्टर का फूरियर रूपांतरण प्रत्येक फ़ंक्शन के फूरियर रूपांतरणों के गुणन के बराबर है:
G { f * g } = ℱ { f } g g { g }
निरंतर फूरियर परिवर्तन के लिए प्रमेय प्रमेय
ℱ { f ( टी ) ( जी ( टी )} = f { एफ ( टी )} * ℱ { जी ( टी )} = एफ ( ω ) * जी ( ω )
ℱ { एफ ( टी ) * जी ( टी )} = f { एफ ( टी )} ⋅ ℱ { जी ( टी )} = एफ ( ω ) ( जी ( ω )
असतत फूरियर रूपांतरण के लिए बातचीत प्रमेय
ℱ { एफ ( एन ) ( जी ( एन )} = f { एफ ( एन )} * ℱ { जी ( एन )} = एफ ( के ) * जी ( के )
ℱ { एफ ( एन ) * जी ( एन )} = f { एफ ( एन )} n ℱ { जी ( एन )} = एफ ( के ) ( जी ( के )
लाप्लास परिवर्तन के लिए कन्वर्सेशन प्रमेय
ℒ { एफ ( टी ) * जी ( टी )} = f { एफ ( टी )} ⋅ ℒ { जी ( टी )} = एफ ( एस ) ( जी ( एस )