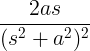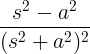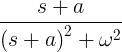लाप्लास ट्रांसफ़ॉर्म

लाप्लास ट्रांसफ़ॉर्मेशन एक समय डोमेन फ़ंक्शन को एस-डोमेन फ़ंक्शन को शून्य से अनंत तक एकीकरण द्वारा परिवर्तित करता है

समय डोमेन समारोह की, से गुणा ई ^-ST ।

लाप्लास ट्रांसफ़ॉर्म का उपयोग अंतर समीकरणों और अभिन्नताओं के समाधान को जल्दी से खोजने के लिए किया जाता है।

समय डोमेन में व्युत्पत्ति s- डोमेन में s द्वारा गुणन में बदल जाती है।

समय डोमेन में एकीकरण s- डोमेन में s द्वारा विभाजन में बदल जाता है।

लाप्लास फ़ंक्शन को रूपांतरित करता है

लाप्लास परिवर्तन एल {} ऑपरेटर के साथ परिभाषित किया गया है :

$F (s) = \ mathcal {L} \ left \ {f (t) \ right \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

उलटा लाप्लास रूपांतरण सीधे गणना की जा सकती है।

आमतौर पर उलटा रूपांतर तालिका से दिया जाता है।

कार्य का नाम	समय डोमेन फ़ंक्शन	लाप्लास परिवर्तन
कार्य का नाम	च ( टी )	F ( s ) = L { f ( t )}
लगातार	1	$\ Frac {1} {s}$
रैखिक	टी	$\ Frac {1} {रों ^ 2}$
शक्ति	t ⁿ	$\ Frac {n!} {रों ^ {n + 1}}$
शक्ति	t ^a	Γ ( एक +1) ⋅ रों ^{- ( एक +1)}
प्रतिपादक	ई ^पर	$\ Frac {1} {} सा$
ज्या	पाप पर	$\ Frac {एक} {रों ^ 2 + एक ^ 2}$
कोसाइन	क्योंकि पर	$\ Frac {s} {s ^ 2 + एक ^ 2}$
हाइपरबोलिक साइन	सिंह पर	$\ Frac {एक} {रों ^ 2-एक ^ 2}$
हाइपरबोलिक कॉशन	सोंटा पर	$\ Frac {s} {s ^ 2-एक ^ 2}$
बढ़ती हुई साइन	टी पाप पर	$\ Frac {2as} {(रों ^ 2 + एक ^ 2) ^ 2}$
बढ़ता हुआ कोसना	t cos पर	$\ Frac {रों ^ 2-एक ^ 2} {(रों ^ 2 + एक ^ 2) ^ 2}$
क्षय होना	e ^-at sin .t	$\ frac {\ _ omega} {\ left (s + a a right) ^ 2 + \ omega ^ 2}$
क्षयकारी कोसाइन	e ^-at cos .t	$\ frac {s + a} {\ left (s + a a right) ^ 2 + \ omega ^ 2}$
डेल्टा समारोह	δ ( टी )	1
विलंबित डेल्टा	δ ( टा )	ई ^-स

सम्पत्ति का नाम	समय डोमेन फ़ंक्शन	लाप्लास परिवर्तन	टिप्पणी
	च ( टी )	एफ ( s )
रैखिकता	एफ ( टी ) + बीजी ( टी )	वायु सेना ( रों ) + बीजी ( रों )	ए , बी स्थिर हैं
स्केल में बदलाव	च ( पर )	$\ frac {1} {a} F \ left (\ frac {s} {a} \ right)$	ए / 0
खिसक जाना	e ^-at f ( t )	एफ ( एस + ए )
विलंब	च ( टा )	ई ^{- के रूप में} एफ ( रों )
व्युत्पत्ति	$\ Frac {df (टी)} {} डीटी$	sF ( s ) - f (0)
एन-वें व्युत्पत्ति	$\ Frac {घ ^ एनएफ (टी)} {डीटी ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
शक्ति	टी ^एन एफ ( टी )	$(-1) ^ n \ frac {घ ^ nF (रों)} {डी एस ^ n}$
एकीकरण	$\ Int_ {0} ^ {टी} f (x) dx$	$\ Frac {1} {s} एफ (रों)$
पारस्परिक	$\ Frac {1} {टी} च (टी)$	$\ int_ {s} ^ {\ infty} F (x) dx$
कनवल्शन	एफ ( टी ) * जी ( टी )	F ( s ) ( G ( s )	* कनविक्शन ऑपरेटर है
आवधिक कार्य	f ( t ) = f ( t + T )	$\ Frac {1} {1-ए ^ {- सेंट}} \ int_ {0} ^ {टी} ई ^ {- sx} f (x) dx$