Másodfokú egyenlet
A másodfokú egyenlet egy másodrendű polinom 3 együtthatóval - a , b , c .
A másodfokú egyenletet a következő adja:
ax 2 + bx + c = 0
A másodfokú egyenlet megoldását 2 x 1 és x 2 szám adja meg .
A másodfokú egyenletet a következő formára változtathatjuk:
( x - x 1 ) ( x - x 2 ) = 0
Másodfokú képlet
A másodfokú egyenlet megoldását a másodfokú képlet adja meg:
![]()
A négyzetgyök belsejében lévő kifejezést diszkriminánsnak nevezzük, és Δ-vel jelöljük:
Δ = b 2 - 4 ac
A másodfokú képlet megkülönböztető jelöléssel:
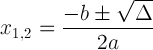
Ez a kifejezés azért fontos, mert elmondhatja nekünk a megoldást:
- Ha Δ/ 0, akkor 2 valós gyök van x 1 = (- b + √ Δ ) / (2a) és x 2 = (- b-√ Δ ) / (2a) .
- Ha Δ = 0, akkor van egy gyök x 1 = x 2 = -b / (2a) .
- Amikor Δ <0, nincsenek valódi gyökerek, 2 komplex gyök van:
x 1 = (- b + i√ -Δ ) / (2a) és x 2 = (- bi√ -Δ ) / (2a) .
1. probléma
3 x 2 +5 x +2 = 0
megoldás:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5-1) / 6 = -6/6 = -1
2. probléma
3 x 2 -6 x +3 = 0
megoldás:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
3. probléma
x 2 +2 x +5 = 0
megoldás:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16) )) / 2
Nincsenek valós megoldások. Az értékek összetett számok:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Másodfokú függvénydiagram
A másodfokú függvény egy másodrendű polinomfüggvény:
f ( x ) = ax 2 + bx + c
A másodfokú egyenlet megoldásai a másodfokú függvény gyökerei, amelyek a másodfokú függvény grafikon metszéspontjai az x tengellyel, amikor
f ( x ) = 0
Ha a grafikonnak az x tengellyel 2 metszéspontja van, akkor a másodfokú egyenletnek két megoldása van.
Ha a grafikonnak az x tengellyel 1 metszéspontja van, akkor a másodfokú egyenletnek 1 megoldása van.
Ha a grafikonnak nincsenek metszéspontjai az x tengellyel, akkor nem valós megoldásokat (vagy 2 komplex megoldást) kapunk.