Természetes logaritmus - ln (x)

A természetes logaritmus a szám e bázisának logaritmusa.

A természetes logaritmus meghatározása

Mikor

e y = x

Ekkor alapozzuk meg x logaritmusát

ln ( x ) = log e ( x ) = y

 

Az e konstans vagy Euler száma:

e ≈ 2,71828183

Ln az exponenciális függvény inverz függvénye

A természetes alapú logaritmus függvény ln (x) az inverz függvény az exponenciális függvény e x .

X/ 0 esetén

f ( f -1 ( x )) = e ln ( x ) = x

Vagy

f -1 ( f ( x )) = ln ( e x ) = x

A természetes logaritmus szabályai és tulajdonságai

Szabály neve Szabály Példa
Termékszabály

ln ( x ∙ y ) = ln ( x ) + ln ( y )

ln (3 ∙ 7) = ln (3) + ln (7)
Kedvező szabály

ln ( x / y ) = ln ( x ) - ln ( y )

ln (3 / 7) = ln (3) - ln (7)
Teljesítményszabály

ln ( x y ) = y ∙ ln ( x )

ln (2 8 ) = 8 ∙ ln (2)
származék
 f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x  
integrál
 ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C  
negatív szám ln
 ln ( x ) nincs meghatározva, ha x ≤ 0  
ln nulla
 ln (0) nincs meghatározva  
 
Az egyikből
 ln (1) = 0  
A végtelen
 lim ln ( x ) = ∞, amikor x → ∞  
Euler kiléte ln (-1) = i π  

 

Logaritmus termékszabály

Az x és y szorzásának logaritmusa az x és y logaritmusának összege.

log b ( x ∙ y ) = log b ( x ) + log b ( y )

Például:

log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)

Logaritmus hányados szabály

Az x és y felosztásának logaritmusa az x és y logaritmusának különbsége.

log b ( x / y ) = log b ( x ) - log b ( y )

Például:

log 10 (3 / 7) = log 10 (3) - log 10 (7)

Logaritmus teljesítményszabálya

Az y hatványára emelt x logaritmusa y szorzója az x logaritmusának.

log b ( x y ) = y ∙ log b ( x )

Például:

log 10 (2 8 ) = 8 ∙ log 10 (2)

A természetes logaritmus származéka

A természetes logaritmusfüggvény deriváltja a reciprokfüggvény.

Mikor

f ( x ) = ln ( x )

Az f (x) származéka:

f ' ( x ) = 1 / x

A természetes logaritmus integrálja

A természetes logaritmusfüggvény integrálját a következők adják meg:

Mikor

f ( x ) = ln ( x )

Az f (x) integrálja:

∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C

Ln 0-ból

A nulla természetes logaritmusa nincs meghatározva:

ln (0) nincs meghatározva

Az x természetes logaritmusának 0-hoz közeli határérték, amikor x megközelíti a nullát, mínusz a végtelen:

1 Ln

Az egyik természetes logaritmusa nulla:

ln (1) = 0

Ln a végtelen

A végtelen természetes logaritmusának határa, amikor x megközelíti a végtelent, megegyezik a végtelennel:

lim ln ( x ) = ∞, amikor x → ∞

Komplex logaritmus

Z komplex szám esetén:

z = re iθ = x + iy

A komplex logaritmus a következő lesz (n = ...- 2, -1,0,1,2, ...):

Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))

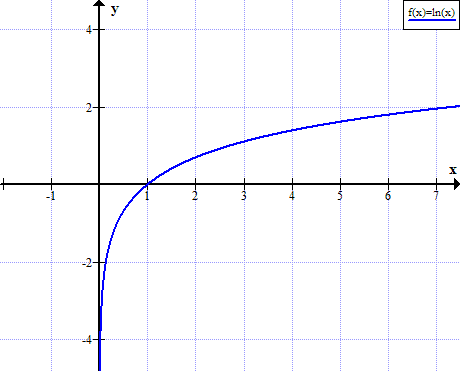
Ln (x) grafikonja

ln (x) nincs meghatározva x valós, nem pozitív értékekre:

Természetes logaritmus táblázat

x ln x
0 határozatlan
0 + - ∞
0,0001 -9,210340
0,001 -6,907755
0,01 -4,605170
0.1 -2,302585
1 0
2 0.693147
e ≈ 2,7183 1
3 1.098612
4 1.386294
5. 1.609438
6. 1,791759
7. 1.945910
8. 2.079442
9. 2.197225
10. 2.302585
20. 2.995732
30. 3.401197
40 3.688879
50 3.912023
60 4.094345
70 4.248495
80 4.382027
90 4.499810
100 4.605170
200 5.298317
300 5.703782
400 5.991465
500 6.214608
600 6.396930
700 6.551080
800 6.684612
900 6.802395
1000 6.907755
10000 9.210340

 

A logaritmus szabályai ►

 

Lásd még

ALGEBRA
GYORS TÁBLÁZATOK