Logaritmusszabályok
A bázis b logaritmus egy szám a kitevő , hogy meg kell emelni a bázis annak érdekében, hogy a számot.
- Logaritmus meghatározása
- A logaritmus szabályai
- Logaritmusproblémák
- Komplex logaritmus
- A napló grafikonja (x)
- Logaritmus táblázat
- Logaritmus kalkulátor
Logaritmus meghatározása
Ha b-t y hatványára emeljük, egyenlő x:
b y = x
Ekkor x b b logaritmusa megegyezik y-vel:
log b ( x ) = y
Például, ha:
2 4 = 16
Akkor
log 2 (16) = 4
Logaritmus, mint az exponenciális függvény inverz függvénye
A logaritmikus függvény,
y = log b ( x )
az exponenciális függvény inverz függvénye,
x = b y
Tehát ha kiszámítjuk az x (x/ 0) logaritmusának exponenciális függvényét,
f ( f -1 ( x )) = b log b ( x ) = x
Vagy ha kiszámítjuk az x exponenciális függvényének logaritmusát,
f -1 ( f ( x )) = log b ( b x ) = x
Természetes logaritmus (ln)
A természetes logaritmus az e bázis logaritmusa:
ln ( x ) = log e ( x )
Amikor e konstans a szám:
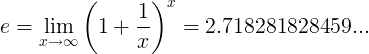
vagy
![]()
Lásd: Természetes logaritmus
Inverz logaritmus számítása
Az inverz logaritmust (vagy antilogaritmust) úgy számoljuk ki, hogy a b alapot y logaritmusra emeljük:
x = log -1 ( y ) = b y
Logaritmikus függvény
A logaritmikus függvény alapformája:
f ( x ) = log b ( x )
A logaritmus szabályai
| Szabály neve | Szabály |
|---|---|
Logaritmus termékszabály |
log b ( x ∙ y ) = log b ( x ) + log b ( y ) |
Logaritmus hányados szabály |
log b ( x / y ) = log b ( x ) - log b ( y ) |
Logaritmus teljesítményszabálya |
log b ( x y ) = y ∙ log b ( x ) |
Logaritmus alapkapcsoló szabály |
log b ( c ) = 1 / log c ( b ) |
Logaritmus alapváltoztatási szabály |
log b ( x ) = log c ( x ) / log c ( b ) |
A logaritmus származéka |
f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b )) |
A logaritmus integrálja |
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C |
Negatív szám logaritmusa |
log b ( x ) nincs meghatározva, ha x ≤ 0 |
0 logaritmusa |
log b (0) nincs meghatározva |
Az 1 logaritmusa |
log b (1) = 0 |
Az alap logaritmusa |
log b ( b ) = 1 |
A végtelenség logaritmusa |
lim log b ( x ) = ∞, amikor x → ∞ |
Lásd: Logaritmusszabályok
Logaritmus termékszabály
Az x és y szorzásának logaritmusa az x és y logaritmusának összege.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Például:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Logaritmus hányados szabály
Az x és y felosztásának logaritmusa az x és y logaritmusának különbsége.
log b ( x / y ) = log b ( x ) - log b ( y )
Például:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Logaritmus teljesítményszabálya
Az y hatványára emelt x logaritmusa y szorzója az x logaritmusának.
log b ( x y ) = y ∙ log b ( x )
Például:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Logaritmus alapkapcsoló szabály
A c b b logaritmusa 1 osztva a b b b logaritmusával.
log b ( c ) = 1 / log c ( b )
Például:
log 2 (8) = 1 / log 8 (2)
Logaritmus alapváltoztatási szabály
Az x b b logaritmusa az x b alap logaritmusa elosztva a b b alap c logaritmusával.
log b ( x ) = log c ( x ) / log c ( b )
Például ahhoz, hogy kiszámítsuk a 2. naplót (8) a számológépben, meg kell változtatnunk az alapot 10-re:
log 2 (8) = log 10 (8) / log 10 (2)
Lásd: naplóalap-változtatási szabály
Negatív szám logaritmusa
Az x b valós logaritmusa, amikor x <= 0, nincs meghatározva, ha x negatív vagy egyenlő nulla:
log b ( x ) nincs meghatározva, ha x ≤ 0
Lásd: negatív szám log
0 logaritmusa
A nulla b b logaritmusa nincs meghatározva:
log b (0) nincs meghatározva
Az x b b logaritmus határértéke, amikor x megközelíti a nullát, mínusz a végtelen:
![]()
Lásd: nulla log
Az 1 logaritmusa
Az egyik b b logaritmusa nulla:
log b (1) = 0
Például az egyik két logaritmusa nulla:
log 2 (1) = 0
Lásd: egy naplója
A végtelenség logaritmusa
Az x b b logaritmus határértéke, amikor x megközelíti a végtelenséget, megegyezik a végtelennel:
lim log b ( x ) = ∞, amikor x → ∞
Lásd: a végtelen naplója
Az alap logaritmusa
B alap b logaritmusa egy:
log b ( b ) = 1
Például a két alap két logaritmusa egy:
log 2 (2) = 1
Logaritmusszármazék
Mikor
f ( x ) = log b ( x )
Ezután az f (x) deriváltja:
f ' ( x ) = 1 / ( x ln ( b ))
Lásd: log derivált
Logaritmus integrál
Az x logaritmusának integrálja:
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
Például:
∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) - 1 / ln (2) ) + C
Logaritmus közelítés
log 2 ( x ) ≈ n + ( x / 2 n - 1),
Komplex logaritmus
Z komplex szám esetén:
z = re iθ = x + iy
A komplex logaritmus a következő lesz (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
Logaritmusproblémák és válaszok
1. probléma
Keresse meg az x elemet
log 2 ( x ) + log 2 ( x -3) = 2
Megoldás:
A termékszabály használata:
log 2 ( x ∙ ( x -3)) = 2
A logaritmus űrlap megváltoztatása a logaritmus meghatározása szerint:
x ∙ ( x -3) = 2 2
Vagy
x 2 -3 x -4 = 0
A másodfokú egyenlet megoldása:
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1
Mivel a logaritmus nincs meghatározva negatív számokra, a válasz a következő:
x = 4
2. probléma
Keresse meg az x elemet
log 3 ( x +2) - log 3 ( x ) = 2
Megoldás:
A hányados szabály használata:
log 3 (( x +2) / x ) = 2
A logaritmus űrlap megváltoztatása a logaritmus meghatározása szerint:
( x +2) / x = 3 2
Vagy
x +2 = 9 x
Vagy
8 x = 2
Vagy
x = 0,25
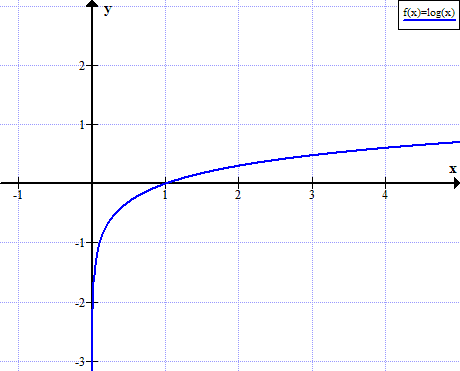
A napló grafikonja (x)
A log (x) nincs meghatározva az x valós, nem pozitív értékeihez:
Logaritmus táblázat
| x | log 10 x | log 2 x | log e x |
|---|---|---|---|
| 0 | határozatlan | határozatlan | határozatlan |
| 0 + | - ∞ | - ∞ | - ∞ |
| 0,0001 | -4 | -13.287712 | -9,210340 |
| 0,001 | -3 | -9,965784 | -6,907755 |
| 0,01 | -2 | -6,643856 | -4,605170 |
| 0.1 | -1 | -3,321928 | -2,302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0,301030 | 1 | 0.693147 |
| 3 | 0.477121 | 1.584963 | 1.098612 |
| 4 | 0,602060 | 2 | 1.386294 |
| 5. | 0.698970 | 2.321928 | 1.609438 |
| 6. | 0.778151 | 2.584963 | 1,791759 |
| 7. | 0,845098 | 2.807355 | 1.945910 |
| 8. | 0,903090 | 3 | 2.079442 |
| 9. | 0,954243 | 3.169925 | 2.197225 |
| 10. | 1 | 3.321928 | 2.302585 |
| 20. | 1.301030 | 4.321928 | 2.995732 |
| 30. | 1.477121 | 4.906891 | 3.401197 |
| 40 | 1.602060 | 5.321928 | 3.688879 |
| 50 | 1.698970 | 5.643856 | 3.912023 |
| 60 | 1.778151 | 5.906991 | 4.094345 |
| 70 | 1,845098 | 6.129283 | 4.248495 |
| 80 | 1.903090 | 6.321928 | 4.382027 |
| 90 | 1.954243 | 6.491853 | 4.499810 |
| 100 | 2 | 6.643856 | 4.605170 |
| 200 | 2.301030 | 7.643856 | 5.298317 |
| 300 | 2.477121 | 8.228819 | 5.703782 |
| 400 | 2.602060 | 8.643856 | 5.991465 |
| 500 | 2.698970 | 8.965784 | 6.214608 |
| 600 | 2.778151 | 9.228819 | 6.396930 |
| 700 | 2.845098 | 9.451211 | 6.551080 |
| 800 | 2.903090 | 9.643856 | 6.684612 |
| 900 | 2.954243 | 9.813781 | 6.802395 |
| 1000 | 3 | 9.965784 | 6.907755 |
| 10000 | 4 | 13.287712 | 9.210340 |
Lásd még
- A logaritmus szabályai
- Az alap logaritmusváltozása
- A nulla logaritmusa
- Az egyik logaritmusa
- A végtelenség logaritmusa
- Negatív szám logaritmusa
- Logaritmus kalkulátor
- Logaritmus grafikon
- Logaritmus táblázat
- Természetes logaritmus kalkulátor
- Természetes logaritmus - ln x
- e állandó
- Decibel (dB)