Konvolúció
A konvolúció az f (τ) korrelációs függvénye a g (t-τ) megfordított függvénnyel.
A konvolúció operátor a csillag szimbólum * .
- Folyamatos konvolúció
- Diszkrét konvolúció
- 2D diszkrét konvolúció
- Szűrés megvalósítása konvolúcióval
- Konvolúciós tétel
Folyamatos konvolúció
F (t) és g (t) konvolúciója egyenlő f (τ) és f (t-τ) szorzóval:
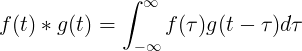
Diszkrét konvolúció
Két diszkrét függvény konvolúciója a következő:
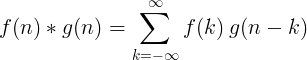
2D diszkrét konvolúció
A képfeldolgozáshoz általában kétdimenziós diszkrét konvolúciót használnak.
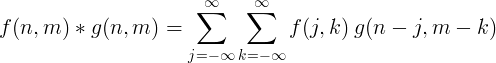
Szűrés megvalósítása konvolúcióval
Szűrhetjük a diszkrét x (n) bemeneti jelet konvolúcióval a h (n) impulzusválasszal az y (n) kimeneti jel megszerzéséhez.
y ( n ) = x ( n ) * h ( n )
Konvolúciós tétel
2 függvény szorzatának Fourier-transzformációja megegyezik az egyes függvények Fourier-transzformációinak konvolúciójával:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
2 függvény konvolúciójának Fourier-transzformációja megegyezik az egyes függvények Fourier-transzformációinak szorzatával:
ℱ { f * g } = ℱ { f } ⋅ ℱ { g }
Konvolúciós tétel a folyamatos Fourier-transzformációhoz
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
Konverziós tétel diszkrét Fourier-transzformációhoz
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
Konvolúciós tétel Laplace-transzformációhoz
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )
Lásd még
SZÁMÍTÁS
- Határ
- Derivált
- Integrál
- Sorozat
- Laplace-transzformáció
- Konvolúció
- Kalkulus szimbólumok
GYORS TÁBLÁZATOK