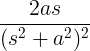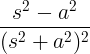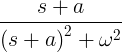Kezdőlap / Matematika / Számítás /Laplace-transzformáció

Laplace Transform

Laplace transzformációs függvény
Laplace transzformációs táblázat
Laplace transzformációs tulajdonságok
Laplace-transzformációs példák

A Laplace-transzformáció egy időtartomány-függvényt s-tartománysá alakít át nulla és végtelen közötti integrációval

az időtartomány függvény értéke, szorozva az e ^{-st értékkel} .

A Laplace-transzformációt arra használják, hogy gyorsan megoldásokat találjanak a differenciálegyenletekre és integrálokra.

Az időtartományban levezetés átalakul s-gyel való szorzásra az s-tartományban.

Az időtartomány integrációja átalakul az s tartományban lévő s osztással.

Laplace transzformációs függvény

A Laplace transzformációt az L {} operátor határozza meg:

$F (s) = \ mathcal {L} \ bal \ {f (t) \ right \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

Fordított Laplace-transzformáció

Az inverz Laplace transzformáció közvetlenül kiszámítható.

Általában az inverz transzformációt a transzformációs táblából adjuk meg.

Laplace transzformációs táblázat

Funkció neve	Időtartomány függvény	Laplace-transzformáció
Funkció neve	f ( t )	F ( s ) = L { f ( t )}
Állandó	1	$\ frac {1} {s}$
Lineáris	t	$\ frac {1} {s ^ 2}$
Erő	t ⁿ	$\ frac {n!} {s ^ {n + 1}}$
Erő	t ^a	Γ ( a +1) ⋅ s ^{- ( a +1)}
Kitevő	e ^at	$\ frac {1} {sa}$
Szinusz	sin at	$\ frac {a} {s ^ 2 + a ^ 2}$
Koszinusz	cos at	$\ frac {s} {s ^ 2 + a ^ 2}$
Hiperbolikus szinusz	sinh at	$\ frac {a} {s ^ 2-a ^ 2}$
Hiperbolikus koszinusz	cosh itt	$\ frac {s} {s ^ 2-a ^ 2}$
Növekvő szinusz	t sin at	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Növekvő koszinusz	t cos at	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Bomló szinusz	e ^-at sin ωt	$\ frac {\ omega} {\ bal (s + a \ jobb) ^ 2 + \ omega ^ 2}$
Bomló koszinusz	e ^-at cos ωt	$\ frac {s + a} {\ balra (s + a \ jobbra) ^ 2 + \ omega ^ 2}$
Delta függvény	δ ( t )	1
Késleltetett delta	δ ( ta )	e ^-as

Laplace transzformációs tulajdonságok

Ingatlan neve	Időtartomány függvény	Laplace-transzformáció	Megjegyzés
	f ( t )	F ( s )
Linearitás	af ( t ) + bg ( t )	aF ( s ) + bG ( s )	a , b állandóak
Méretváltozás	f ( at )	$\ frac {1} {a} F \ balra (\ frac {s} {a} \ jobbra)$	a / 0
Váltás	e ^-at f ( t )	F ( s + a )
Késleltetés	f ( ta )	e ^{- mint} F ( s )
Származtatás	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
N-edik levezetés	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
Erő	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Integráció	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (ek)$
Kölcsönös	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
Konvolúció	f ( t ) * g ( t )	F ( s ) ⋅ G ( s )	* a konvolúció operátor
Periodikus funkció	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$

Laplace-transzformációs példák

1. példa

Keresse meg f (t) transzformációját:

f ( t ) = 3 t + 2 t ²

Megoldás:

ℒ { t } = 1 / s ²

ℒ { t ² } = 2 / s ³

F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t ² } = 3ℒ { t } + 2ℒ { t ² } = 3 / s ² + 4 / s ³

2. példa

Keresse meg F (s) inverz transzformációját:

F ( s ) = 3 / ( s ² + s - 6)

Megoldás:

Az inverz transzformáció megtalálásához az s tartományfüggvényt egyszerűbb formára kell cserélnünk:

F ( s ) = 3 / ( s ² + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)

[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]

a ( s +3) + b ( s -2) = 3

Az a és b megtalálásához 2 egyenletet kapunk - az s együttható egyikét, a többit pedig a másodikból:

( a + b ) s + 3 a -2 b = 3

a + b = 0, 3 a -2 b = 3

a = 3/5, b = -3/5

F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)

Most F (ek) könnyen transzformálható a transzformátorok táblázata segítségével az exponens függvényhez:

f ( t ) = (3/5) e ^{2 t} - (3/5) e ^{-3 t}

Lásd még

SZÁMÍTÁS

GYORS TÁBLÁZATOK