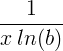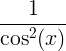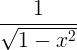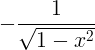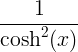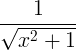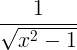Származtatott szabályok

Származtatott szabályok és törvények. A függvények származtatott táblázata.

Származtatott meghatározás

A függvény deriváltja az f (x) függvényérték különbségének aránya az x + Δx és x pontokban a Δx-szel, amikor Δx végtelenül kicsi. A derivált az érintő egyenes függvénylejtése vagy meredeksége az x pontban.

 

f '(x) = \ lim _ {\ Delta x \ to 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}

Második származék

A második származékot a következők adják:

Vagy egyszerűen származtassa az első származékot:

f

N-dik derivált

Az n- dik deriváltot f (x) n-szer levezetésével számoljuk.

Az n- dik származék egyenlő az (n-1) származék származékával:

f ( n ) ( x ) = [ f ( n -1) ( x )] '

Példa:

Keresse meg a negyedik deriváltját

f ( x ) = 2 x 5

f (4) ( x ) = [2 x 5 ] "" "= [10 x 4 ]" "= [40 x 3 ]" = [120 x 2 ] '= 240 x

Származék a függvény grafikonján

A függvény deriváltja a tangenciális egyenes meredeksége.

Származtatott szabályok

Származtatott összeg szabály

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Származtatott termék szabály

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Származtatott hányados szabály 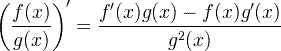\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}
Származtatott láncszabály

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Származtatott összeg szabály

Amikor a és b konstansok.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Példa:

Keresse meg a következő származékát:

3 x 2 + 4 x.

Az összegszabály szerint:

a = 3, b = 4

f ( x ) = x 2 , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Származtatott termék szabály

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Származtatott hányados szabály

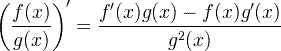
\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}

Származtatott láncszabály

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Ez a szabály jobban érthető Lagrange jelölésével:

\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}

Funkció lineáris közelítés

Kis Δx esetén közelítést kaphatunk f (x 0 + Δx) -hez, ha ismerjük f (x 0 ) és f '(x 0 ):

f ( x 0 + Δ x ) ≈ f ( x 0 ) + F „( x 0 ) ⋅Δ X

A függvények származtatott táblázata

Funkció neve Funkció Derivált

f ( x )

 f '( x )
Állandó

konst

0

Lineáris

x

1

Erő

x a

ax a- 1
Exponenciális

e x

e x
Exponenciális

a x

a x ln a
Természetes logaritmus

ln ( x )

Logaritmus

log b ( x )

Szinusz

bűn x

cos x
Koszinusz

cos x

-sin x
Tangens

tan x

Arcsine

arcsin x

Arccosine

arccos x

Arctangent

arctan x
Hiperbolikus szinusz

sinh x

cosh x
Hiperbolikus koszinusz

cosh x

sinh x
Hiperbolikus érintő

tanh x

Inverz hiperbolikus szinusz

sinh -1 x

Inverz hiperbolikus koszinusz

cosh -1 x

Inverz hiperbolikus érintő

tanh -1 x

Származtatott példák

1. példa

f ( x ) = x 3 +5 x 2 + x +8

f ' ( x ) = 3 x 2 + 2 ~ 5 x + 1 + 0 = 3 x 2 +10 x +1

2. példa

f ( x ) = bűn (3 x 2 )

A láncszabály alkalmazásakor:

f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x

Második derivált teszt

Amikor egy függvény első deriváltja nulla az x 0 pontban .

f '( x 0 ) = 0

Ekkor az x 0 pont második deriváltja , f '' (x 0 ), jelezheti az adott pont típusát:

 

f '' ( x 0 )/ 0

 helyi minimum

f '' ( x 0 ) <0

 helyi maximum

f "" ( x 0 ) = 0

 meghatározatlan

 

Lásd még

SZÁMÍTÁS
GYORS TÁBLÁZATOK