Logaritma Natural - ln (x)
Logaritma natural adalah logaritma ke basis e sebuah bilangan.
- Definisi logaritma natural (ln)
- Aturan & properti logaritma natural (ln)
- Logaritma kompleks
- Grafik ln (x)
- Tabel logaritma natural (ln)
- Kalkulator logaritma natural
Definisi logaritma natural
Kapan
e y = x
Maka basis e logaritma dari x adalah
ln ( x ) = log e ( x ) = y
The e konstan atau nomor Euler adalah:
e ≈ 2,71828183
Ln sebagai fungsi kebalikan dari fungsi eksponensial
Fungsi logaritma natural ln (x) adalah fungsi kebalikan dari fungsi eksponensial e x .
Untuk x/ 0,
f ( f -1 ( x )) = e ln ( x ) = x
Atau
f -1 ( f ( x )) = ln ( e x ) = x
Aturan dan properti logaritma natural
| Nama aturan | Aturan | Contoh |
|---|---|---|
Aturan produk |
ln ( x ∙ y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
Aturan hasil bagi |
ln ( x / y ) = ln ( x ) - ln ( y ) |
ln (3 / 7) = ln (3) - ln (7) |
Aturan kekuasaan |
ln ( x y ) = y ∙ ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
Dalam turunan |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
ln integral |
∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C. | |
Dalam angka negatif |
ln ( x ) tidak terdefinisi saat x ≤ 0 | |
Di nol |
ln (0) tidak ditentukan | |
salah satu |
ln (1) = 0 | |
Dalam jumlah tak terbatas |
lim ln ( x ) = ∞, ketika x → ∞ | |
| Identitas Euler | ln (-1) = i π |
Aturan hasil kali logaritma
Logaritma dari perkalian x dan y adalah jumlah dari logaritma dari x dan logaritma dari y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Sebagai contoh:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Aturan hasil bagi logaritma
Logaritma dari pembagian x dan y adalah selisih logaritma dari x dan logaritma y.
log b ( x / y ) = log b ( x ) - log b ( y )
Sebagai contoh:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Aturan kekuatan logaritma
Logaritma dari x yang dipangkatkan dari y adalah y dikali logaritma dari x.
log b ( x y ) = y ∙ log b ( x )
Sebagai contoh:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Turunan dari logaritma natural
Turunan dari fungsi logaritma natural adalah fungsi timbal balik.
Kapan
f ( x ) = ln ( x )
Turunan dari f (x) adalah:
f ' ( x ) = 1 / x
Integral dari logaritma natural
Integral dari fungsi logaritma natural diberikan oleh:
Kapan
f ( x ) = ln ( x )
Integral dari f (x) adalah:
∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C
Ln dari 0
Logaritma natural dari nol tidak ditentukan:
ln (0) tidak ditentukan
Batas mendekati 0 dari logaritma natural x, ketika x mendekati nol, minus tak terhingga:
![]()
Ln dari 1
Logaritma natural dari satu adalah nol:
ln (1) = 0
Ln tak terhingga
Batas dari logaritma natural tak terhingga, ketika x mendekati tak terhingga sama dengan tak terhingga:
lim ln ( x ) = ∞, ketika x → ∞
Logaritma kompleks
Untuk bilangan kompleks z:
z = re iθ = x + iy
Logaritma kompleks akan menjadi (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
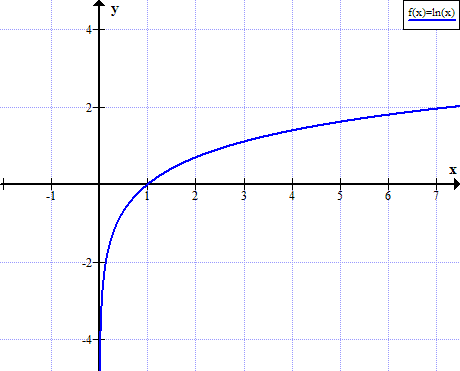
Grafik ln (x)
ln (x) tidak ditentukan untuk nilai non positif nyata dari x:
Tabel logaritma natural
| x | ln x |
|---|---|
| 0 | tidak terdefinisi |
| 0 + | - ∞ |
| 0,0001 | -9.210340 |
| 0,001 | -6,907755 |
| 0,01 | -4.605170 |
| 0.1 | -2.302585 |
| 1 | 0 |
| 2 | 0,693147 |
| e ≈ 2.7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1.791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2. 197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |
Lihat juga
- Logaritma (log)
- Kalkulator logaritma natural
- Logaritma natural nol
- Logaritma natural salah satunya
- Logaritma natural dari e
- Logaritma natural tak terhingga
- Logaritma natural dari bilangan negatif
- Fungsi invers ln
- grafik ln (x)
- Tabel logaritma natural
- Kalkulator logaritma
- e konstan
ALJABAR
TABEL CEPAT