Lilitan

Konvolusi adalah fungsi korelasi f (τ) dengan fungsi terbalik g (t-τ).

Operator konvolusi adalah simbol asterisk * .

Konvolusi f (t) dan g (t) sama dengan integral dari f (τ) kali f (t-τ):

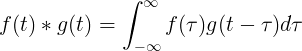
$f (t) * g (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) d \ tau$

Konvolusi dari 2 fungsi diskrit didefinisikan sebagai:

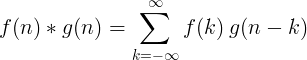
$f (n) * g (n) = \ sum_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)$

Konvolusi diskrit 2 dimensi biasanya digunakan untuk pemrosesan gambar.

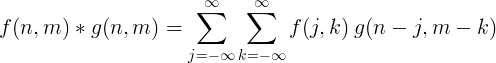
$f (n, m) * g (n, m) = \ sum_ {j = - \ infty} ^ {\ infty} \ sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: g (nj, mk)$

Kita dapat menyaring sinyal masukan diskrit x (n) dengan konvolusi dengan respon impuls h (n) untuk mendapatkan sinyal keluaran y (n).

y ( n ) = x ( n ) * h ( n )

Transformasi Fourier dari perkalian 2 fungsi sama dengan konvolusi transformasi Fourier setiap fungsi:

ℱ { f ⋅ g } = ℱ { f } * ℱ { g }

Transformasi Fourier dari sebuah lilitan 2 fungsi sama dengan perkalian transformasi Fourier dari setiap fungsi:

ℱ { f * g } = ℱ { f } ⋅ ℱ { g }

ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )

ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )

ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )

ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )

Lihat juga