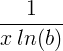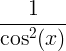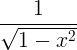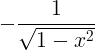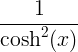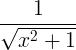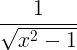Aturan turunan
Aturan dan hukum turunan. Derivatif tabel fungsi.
Definisi turunan
Turunan dari suatu fungsi adalah rasio selisih nilai fungsi f (x) pada titik x + Δx dan x dengan Δx, jika Δx sangat kecil. Turunannya adalah fungsi kemiringan atau kemiringan garis singgung pada titik x.
![]()
Turunan kedua
Turunan kedua diberikan oleh:
![]()
Atau cukup turunkan turunan pertamanya:
![]()
Turunan ke-n
The n turunan th dihitung dengan menurunkan f (x) n kali.
The n th yaitu turunan sama dengan turunan dari (n-1) turunan:
f ( n ) ( x ) = [ f ( n -1) ( x )] '
Contoh:
Temukan turunan keempat dari
f ( x ) = 2 x 5
f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x
Turunan dari grafik fungsi
Turunan dari suatu fungsi adalah slop dari garis tangensial.
Aturan turunan
| Aturan jumlah turunan | ( af ( x ) + bg ( x )) '= f' ( x ) + bg ' ( x ) |
| Aturan produk turunan | ( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| Aturan hasil bagi turunan | 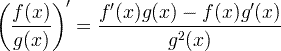 |
| Aturan rantai turunan | f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
Aturan jumlah turunan
Ketika a dan b adalah konstanta.
( af ( x ) + bg ( x )) '= f' ( x ) + bg ' ( x )
Contoh:
Temukan turunan dari:
3 x 2 + 4 x.
Menurut aturan penjumlahan:
a = 3, b = 4
f ( x ) = x 2 , g ( x ) = x
f ' ( x ) = 2 x , g' ( x ) = 1
(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4
Aturan produk turunan
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Aturan hasil bagi turunan
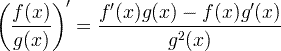
Aturan rantai turunan
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
Aturan ini bisa lebih dipahami dengan notasi Lagrange:
![]()
Pendekatan linier fungsi
Untuk Δx kecil, kita bisa mendapatkan pendekatan ke f (x 0 + Δx), jika kita mengetahui f (x 0 ) dan f '(x 0 ):
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x
Derivatif tabel fungsi
| Nama fungsi | Fungsi | Turunan |
|---|---|---|
| f ( x ) |
f '( x ) | |
| Konstan | const |
0 |
| Linear | x |
1 |
| Kekuasaan | x a |
kapak a- 1 |
| Eksponensial | e x |
e x |
| Eksponensial | a x |
a x ln a |
| Logaritma natural | ln ( x ) |
|
| Logaritma | log b ( x ) |
|
| Sinus | sin x |
cos x |
| Kosinus | cos x |
-sin x |
| Garis singgung | tan x |
|
| Arcsine | arcsin x |
|
| Arccosine | arccos x |
|
| Arktangen | arctan x |
|
| Sinus hiperbolik | sinh x |
cosh x |
| Kosinus hiperbolik | cosh x |
sinh x |
| Garis singgung hiperbolik | tanh x |
|
| Sinus hiperbolik terbalik | sinh -1 x |
|
| Kosinus hiperbolik terbalik | cosh -1 x |
|
| Garis singgung hiperbolik terbalik | tanh -1 x |
|
Contoh turunan
Contoh 1
f ( x ) = x 3 +5 x 2 + x +8
f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
Contoh # 2
f ( x ) = sin (3 x 2 )
Saat menerapkan aturan rantai:
f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x
Tes turunan kedua
Saat turunan pertama suatu fungsi adalah nol pada titik x 0 .
f '( x 0 ) = 0
Maka turunan keduanya pada titik x 0 , f '' (x 0 ), dapat menunjukkan jenis titik tersebut:
| f '' ( x 0 )/ 0 |
minimum lokal |
| f '' ( x 0 ) <0 |
maksimum lokal |
| f '' ( x 0 ) = 0 |
yg tak dpt ditentukan |