Varianza

In probabilità e statistica, la varianza di una variabile casuale è il valore medio della distanza quadrata dal valore medio. Rappresenta il modo in cui la variabile casuale è distribuita vicino al valore medio. Una piccola varianza indica che la variabile casuale è distribuita vicino al valore medio. La grande varianza indica che la variabile casuale è distribuita lontano dal valore medio. Ad esempio, con la distribuzione normale, la curva a campana stretta avrà una piccola varianza e la curva a campana larga avrà una grande varianza.

Definizione di varianza

La varianza della variabile casuale X è il valore atteso dei quadrati di differenza di X e il valore atteso μ.

σ 2 = Var ( X ) = E [( X - μ ) 2 ]

Dalla definizione della varianza possiamo ricavare

σ 2 = Var ( X ) = E ( X 2 ) - μ 2

Varianza della variabile casuale continua

Per variabile casuale continua con valore medio μ e funzione di densità di probabilità f (x):

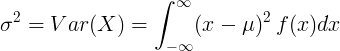
\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx

o

Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2

Varianza della variabile casuale discreta

Per la variabile casuale discreta X con valore medio μ e funzione di massa di probabilità P (x):

\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)

o

Var (X) = \ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2

Proprietà della varianza

Quando X e Y sono variabili casuali indipendenti:

Var ( X + Y ) = Var ( X ) + Var ( Y )

 

Deviazione standard ►

 

Guarda anche

PROBABILITÀ E STATISTICHE
TAVOLI RAPIDI