Distribuzione di probabilità

In probabilità e statistica la distribuzione è una caratteristica di una variabile casuale, descrive la probabilità della variabile casuale in ogni valore.

Ogni distribuzione ha una determinata funzione di densità di probabilità e una funzione di distribuzione di probabilità.

Sebbene ci sia un numero indefinito di distribuzioni di probabilità, ci sono diverse distribuzioni comuni in uso.

Funzione di distribuzione cumulativa

La distribuzione di probabilità è descritta dalla funzione di distribuzione cumulativa F (x),

che è la probabilità della variabile casuale X di ottenere un valore minore o uguale a x:

F ( x ) = P ( X ≤ x )

Distribuzione continua

La funzione di distribuzione cumulativa F (x) è calcolata dall'integrazione della funzione di densità di probabilità f (u) della variabile casuale continua X.

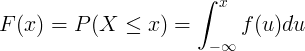
Distribuzione discreta

La funzione di distribuzione cumulativa F (x) è calcolata sommando la funzione massa di probabilità P (u) della variabile casuale discreta X.

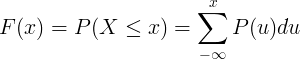
Tabella delle distribuzioni continue

La distribuzione continua è la distribuzione di una variabile casuale continua.

Esempio di distribuzione continua

...

Tabella delle distribuzioni continue

Nome della distribuzione Simbolo di distribuzione Funzione densità di probabilità (pdf) Significare Varianza
   

f X ( x )

μ = E ( X )

σ 2 = Var ( X )
Normale / gaussiana

X ~ N (μ, σ 2 )

 \ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}} μ σ 2
Uniforme

X ~ U ( a , b )

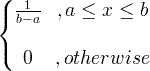 \ begin {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, altrimenti \ end {matrix} \ frac {(ba) ^ 2} {12}
Esponenziale X ~ exp (λ) \ begin {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {matrix} \ frac {1} {\ lambda} \ frac {1} {\ lambda ^ 2}
Gamma X ~ gamma ( c , λ) 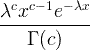\ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {\ Gamma (c)}

x / 0, c / 0, λ/ 0

 \ frac {c} {\ lambda} \ frac {c} {\ lambda ^ 2}
Chi quadrato

X ~ χ 2 ( k )

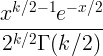 \ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} \ Gamma (k / 2)}

k

2 k
Wishart        
F

X ~ F ( k 1 , k 2 )

      
Beta        
Weibull        
Log-normale

X ~ LN (μ, σ 2 )

      
Rayleigh        
Cauchy        
Dirichlet        
Laplace        
Levy        
Riso        
Student's t        

Tabella delle distribuzioni discrete

La distribuzione discreta è la distribuzione di una variabile casuale discreta.

Esempio di distribuzione discreta

...

Tabella delle distribuzioni discrete

Nome della distribuzione Simbolo di distribuzione Probabilità funzione di massa (pmf) Significare Varianza
    f x ( k ) = P ( X = k )

k = 0,1,2, ...

 E ( x ) Var ( x )
Binomiale

X ~ Bin ( n , p )

 \ binom {n} {k} p ^ {k} (1-p) ^ {nk}

np

np (1- p )
Poisson

X ~ Poisson (λ)

λ ≥ 0

λ

λ

Uniforme

X ~ U ( a, b )

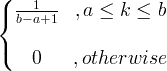 \ begin {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, altrimenti \ end {matrix} \ frac {a + b} {2} \ frac {(b-a + 1) ^ {2} -1} {12}
Geometrico

X ~ Geom ( p )

 p (1-p) ^ {k}

\ frac {1-p} {p}

\ frac {1-p} {p ^ 2}
Iper-geometrico

X ~ HG ( N , K , n )

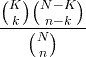N = 0,1,2, ...

K = 0,1, .., N

n = 0,1, ..., N

 \ frac {nK} {N} \ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}
Bernoulli

X ~ Berna ( p )

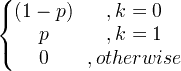 \ begin {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, altrimenti \ end {matrix}

p

p (1- p )

 

Guarda anche

PROBABILITÀ E STATISTICHE
TAVOLI RAPIDI