二次方程式
二次方程式は、3つの係数(a、b、c)を持つ2次多項式です。
二次方程式は次の式で与えられます。
ax 2 + bx + c = 0
二次方程式の解は、2つの数値xで与えられる1及びX 2。
二次方程式を次の形式に変更できます。
(x - x 1)(x - x 2)= 0
二次方程式
二次方程式の解は、二次方程式で与えられます。
![]()
平方根内の式は判別式と呼ばれ、Δで表されます。
Δ= B 2 - 4 AC
判別表記の2次方程式:
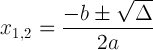
この式は、解決策について教えてくれるので重要です。
- Δ/ 0は、2本の実根が存在する場合、X 1 =( - B +√ Δ)/(2a)及びX 2 =( - B-√ Δ)/(2A) 。
- Δ= 0の場合、1つの根x 1 = x 2 = -b /(2a)があります。
- :Δ<0は、本当の根が存在しない場合、2つの複素根あり
、X 1( - B +i√= -Δ)/(2a)及びX 2 =( - bi√ -Δ)/(2A) 。
問題#1
3 x 2 +5 x +2 = 0
解決:
a = 3、b = 5、c = 2
X 1,2 =(-5±√(5 2 - 4×3×2))/(2×3)=(-5±√(25-24))/ 6 =(-5±1)/ 6
x 1 =(-5 + 1)/ 6 = -4/6 = -2/3
x 2 =(-5-1)/ 6 = -6/6 = -1
問題#2
3 x 2 -6 x +3 = 0
解決:
a = 3、b = -6、c = 3
X 1,2 =(6±√((-6)2 - 4×3×3))/(2×3)=(6±√(36-36))/ 6 =(6±0)/ 6
x 1 = x 2 = 1
問題#3
x 2 +2 x +5 = 0
解決:
a = 1、b = 2、c = 5
X 1,2 =(-2±√(2 2 - 4×1×5))/(2×1)=(-2±√(4-20))/ 2 =(-2±√(-16 ))/ 2
実際の解決策はありません。値は複素数です。
x 1 = -1 + 2 i
x 2 = -1-2 i
二次関数グラフ
二次関数は2次多項式関数です。
f(x)= ax 2 + bx + c
二次方程式の解は、二次関数の根です。これは、二次関数グラフとx軸の交点です。
f(x)= 0
グラフとx軸の交点が2つある場合、2次方程式には2つの解があります。
グラフとx軸の交点が1つある場合、2次方程式の解は1つあります。
グラフとx軸の交点がない場合、実際の解(または2つの複雑な解)は得られません。