対数の公式
数値の基数bの対数は、数値を取得するために基数を上げる必要がある指数です。
対数の定義
bをyの累乗にすると、xは次のようになります。
b y = x
次に、xの基数bの対数はyに等しくなります。
log b(x)= y
たとえば、次の場合です。
2 4 = 16
次に
ログ2(16)= 4
指数関数の逆関数としての対数
対数関数、
y = log b(x)
は指数関数の逆関数であり、
x = b y
したがって、x(x/ 0)の対数の指数関数を計算すると、
f(f -1(x))= b log b (x) = x
または、xの指数関数の対数を計算すると、
f -1(f(x))= log b(b x)= x
自然対数(ln)
ln(x)= log e(x)
ときに電子定数は数あります:
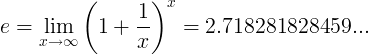
または
![]()
参照:自然対数
逆対数計算
逆対数(または真数)は、基数bを対数yに上げることによって計算されます。
x = log -1(y)= b y
対数関数
対数関数の基本的な形式は次のとおりです。
f(x)= log b(x)
対数の公式
| ルール名 | ルール |
|---|---|
対数積の法則 |
log b(x∙y)= log b(x)+ log b(y) |
対数商の法則 |
ログB(X / Y)=ログB(X)-ログB(Y) |
対数べき乗則 |
ログB(XがYを)= yが∙ログBの(X) |
対数ベーススイッチルール |
log b(c)= 1 / log c(b) |
対数ベース変更規則 |
log b(x)= log c(x)/ log c(b) |
対数微分 |
f(x)= log b(x) ⇒f '(x)= 1 /(x ln(b)) |
対数積分 |
∫ ログB(X)DX = X∙(ログB(X) - 1 / LN(B) )+ C |
負の数の対数 |
ログB(Xが)定義されていない場合 、X ≤0 |
0の対数 |
log b(0)は未定義です |
1の対数 |
log b(1)= 0 |
ベースの対数 |
log b(b)= 1 |
無限大の対数 |
lim log b(x)= ∞、x →∞の場合 |
参照:対数の公式
対数積の法則
xとyの乗算の対数は、xの対数とyの対数の合計です。
log b(x∙y)= log b(x)+ log b(y)
例えば:
log 10(3 ∙ 7)= log 10(3)+ log 10(7)
対数商の法則
xとyの除算の対数は、xの対数とyの対数の差です。
ログB(X / Y)=ログB(X)-ログB(Y)
例えば:
ログ10(3 / 7)=ログ10(3)-ログ10(7)
対数べき乗則
xの対数をyの累乗にすると、yはxの対数の倍になります。
ログB(XがYを)= yが∙ログBの(X)
例えば:
ログ10(2 8)= 8 ∙ログ10(2)
対数ベーススイッチルール
cの基数bの対数は、1をbの基数cの対数で割ったものです。
log b(c)= 1 / log c(b)
例えば:
ログ2(8)= 1 /ログ8(2)
対数ベース変更規則
xの基数bの対数は、xの基数cの対数をbの基数cの対数で割ったものです。
log b(x)= log c(x)/ log c(b)
たとえば、電卓でlog 2(8)を計算するには、底を10に変更する必要があります。
ログ2(8)=ログ10(8)/ログ10(2)
参照:底の変換公式
負の数の対数
xが負またはゼロに等しい場合、x <= 0の場合のxの基数bの実数対数は未定義です。
ログB(Xが)定義されていない場合 、X ≤0
参照:負の数のログ
0の対数
ゼロの基数bの対数は未定義です:
log b(0)は未定義です
xがゼロに近づくときのxの底b対数の限界は、マイナス無限大です。
![]()
参照:ゼロのログ
1の対数
1の基数bの対数はゼロです。
log b(1)= 0
たとえば、1の基数2の対数はゼロです。
ログ2(1)= 0
参照:1つのログ
無限大の対数
xが無限大に近づくときのxの底b対数の限界は、無限大に等しくなります。
lim log b(x)=∞、x →∞の場合
参照:無限の対数
ベースの対数
bの基数bの対数は次のとおりです。
log b(b)= 1
たとえば、2の基数2の対数は1です。
log 2(2)= 1
対数微分
いつ
f(x)= log b(x)
次に、f(x)の導関数:
f '(x)= 1 /(x ln(b))
参照:対数微分
対数積分
xの対数積分:
∫ ログB(X)DX = X∙(ログB(X) - 1 / LN(B) )+ C
例えば:
∫ ログ2(X)DX = X∙(ログ2(X) - 1 / LN(2) )+ Cを
対数近似
ログ2(X)≈ N +(X / 2 N - 1)
複素対数
複素数zの場合:
z = reiθ = x + iy
複素数の対数は次のようになります(n = ...- 2、-1,0,1,2、...):
Log z = ln(r)+ i(θ+2nπ)= ln(√(x 2 + y 2))+ i・arctan(y / x))
対数の問題と回答
問題#1
xを探す
log 2(x)+ log 2(x -3)= 2
解決:
製品ルールの使用:
log 2(x∙(x -3))= 2
対数の定義に従って対数形式を変更します。
x∙(x -3)= 2 2
または
x 2 -3 x -4 = 0
二次方程式を解く:
x 1,2 = [3±√(9 + 16)] / 2 = [3±5] / 2 = 4、-1
負の数には対数が定義されていないため、答えは次のとおりです。
x = 4
問題#2
xを探す
log 3(x +2)-log 3(x)= 2
解決:
商の法則の使用:
log 3((x +2)/ x)= 2
対数の定義に従って対数形式を変更します。
(x +2)/ x = 3 2
または
x +2 = 9 x
または
8 x = 2
または
x = 0.25
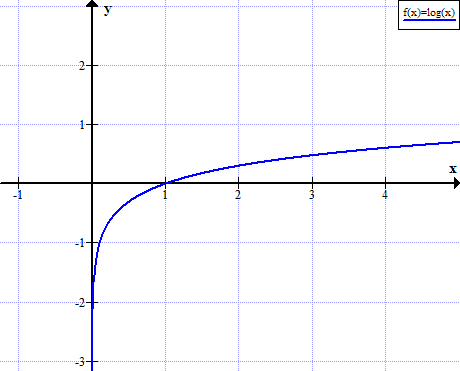
log(x)のグラフ
log(x)は、xの実際の非正の値に対して定義されていません。
対数表
| x | ログ10のxを | ログイン2のxを | log e x |
|---|---|---|---|
| 0 | 未定義 | 未定義 | 未定義 |
| 0 + | -∞ | -∞ | -∞ |
| 0.0001 | -4 | -13.287712 | -9.210340 |
| 0.001 | -3 | -9.965784 | -6.907755 |
| 0.01 | -2 | -6.643856 | -4.605170 |
| 0.1 | -1 | -3.321928 | -2.302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0.301030 | 1 | 0.693147 |
| 3 | 0.477121 | 1.584963 | 1.098612 |
| 4 | 0.602060 | 2 | 1.386294 |
| 5 | 0.698970 | 2.321928 | 1.609438 |
| 6 | 0.778151 | 2.584963 | 1.791759 |
| 7 | 0.845098 | 2.807355 | 1.945910 |
| 8 | 0.903090 | 3 | 2.079442 |
| 9 | 0.954243 | 3.169925 | 2.197225 |
| 10 | 1 | 3.321928 | 2.302585 |
| 20 | 1.301030 | 4.321928 | 2.995732 |
| 30 | 1.477121 | 4.906891 | 3.401197 |
| 40 | 1.602060 | 5.321928 | 3.688879 |
| 50 | 1.698970 | 5.643856 | 3.912023 |
| 60 | 1.778151 | 5.906991 | 4.094345 |
| 70 | 1.845098 | 6.129283 | 4.248495 |
| 80 | 1.903090 | 6.321928 | 4.382027 |
| 90 | 1.954243 | 6.491853 | 4.499810 |
| 100 | 2 | 6.643856 | 4.605170 |
| 200 | 2.301030 | 7.643856 | 5.298317 |
| 300 | 2.477121 | 8.228819 | 5.703782 |
| 400 | 2.602060 | 8.643856 | 5.991465 |
| 500 | 2.698970 | 8.965784 | 6.214608 |
| 600 | 2.778151 | 9.228819 | 6.396930 |
| 700 | 2.845098 | 9.451211 | 6.551080 |
| 800 | 2.903090 | 9.643856 | 6.684612 |
| 900 | 2.954243 | 9.813781 | 6.802395 |
| 1000 | 3 | 9.965784 | 6.907755 |
| 10000 | 4 | 13.287712 | 9.210340 |