自然対数-ln(x)
自然対数は、数値の底eに対する対数です。
自然対数の定義
いつ
e y = x
次に、xの基数e対数は
ln(x)= log e(x)= y
電子定数やオイラー数は、次のとおりです。
E ≈2.71828183
指数関数の逆関数としてのLn
自然対数関数LN(x)は、指数関数eの逆関数であるX。
x/ 0の場合、
f(f -1(x))= e ln(x) = x
または
f -1(f(x))= ln(e x)= x
自然対数のルールとプロパティ
| ルール名 | ルール | 例 |
|---|---|---|
積の法則 |
ln(x∙y)= ln(x)+ ln(y) |
ln(3 ∙ 7)= ln(3)+ ln(7) |
商の法則 |
LN(X / Y)= LN(X)- LN(Y) |
LN(3 / 7)= LN(3)- LN(7) |
べき乗則 |
ln(x y)= y∙ ln(x) |
ln(2 8)= 8 ∙ ln(2) |
ln導関数 |
f(x)= ln(x) ⇒f '(x)= 1 / x | |
ln積分 |
∫ln (x)dx = x∙(ln(x)-1)+ C | |
負の数のln |
LN(Xは)未定義の場合 、X ≤0 | |
ゼロのln |
ln(0)は未定義です | |
1つのln |
ln(1)= 0 | |
無限大のln |
lim ln(x)=∞、x →∞の場合 | |
| オイラーの等式 | LN(-1)= I π |
対数積の法則
xとyの乗算の対数は、xの対数とyの対数の合計です。
log b(x∙y)= log b(x)+ log b(y)
例えば:
log 10(3 ∙ 7)= log 10(3)+ log 10(7)
対数商の法則
xとyの除算の対数は、xの対数とyの対数の差です。
ログB(X / Y)=ログB(X)-ログB(Y)
例えば:
ログ10(3 / 7)=ログ10(3)-ログ10(7)
対数べき乗則
xの対数をyの累乗にすると、yはxの対数の倍になります。
ログB(XがYを)= yが∙ログBの(X)
例えば:
ログ10(2 8)= 8 ∙ログ10(2)
自然対数の導関数
自然対数関数の導関数は相互関数です。
いつ
f(x)= ln(x)
f(x)の導関数は次のとおりです。
f '(x)= 1 / x
自然対数の積分
自然対数関数の積分は次の式で与えられます。
いつ
f(x)= ln(x)
f(x)の積分は次のとおりです。
∫ F(X)DX =∫ LN(X)DX = X∙(LN(X) - 1)+ C
0のLn
ゼロの自然対数は定義されていません。
ln(0)は未定義です
xがゼロに近づくとき、xの自然対数の0に近い限界は、マイナス無限大です。
![]()
1のLn
1の自然対数はゼロです。
ln(1)= 0
無限のLn
xが無限大に近づくときの無限大の自然対数の限界は、無限大に等しくなります。
lim ln(x)=∞、x →∞の場合
複素対数
複素数zの場合:
z = reiθ = x + iy
複素数の対数は次のようになります(n = ...- 2、-1,0,1,2、...):
Log z = ln(r)+ i(θ+2nπ)= ln(√(x 2 + y 2))+ i・arctan(y / x))
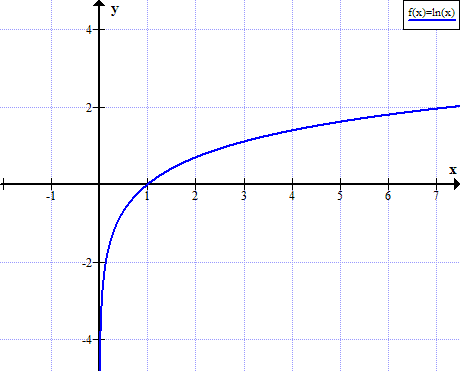
ln(x)のグラフ
ln(x)は、xの実際の非正の値に対して定義されていません。
自然対数表
| x | ln x |
|---|---|
| 0 | 未定義 |
| 0 + | -∞ |
| 0.0001 | -9.210340 |
| 0.001 | -6.907755 |
| 0.01 | -4.605170 |
| 0.1 | -2.302585 |
| 1 | 0 |
| 2 | 0.693147 |
| E ≈2.7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1.791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |