畳み込み
畳み込みは、f(τ)と逆関数g(t-τ)の相関関数です。
畳み込み演算子はアスタリスク記号*です。
連続畳み込み
f(t)とg(t)の畳み込みは、f(τ)×f(t-τ)の積分に等しくなります。
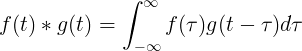
離散たたみ込み
2つの離散関数の畳み込みは次のように定義されます。
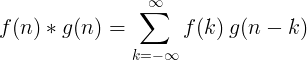
2D離散畳み込み
通常、画像処理には2次元の離散畳み込みが使用されます。
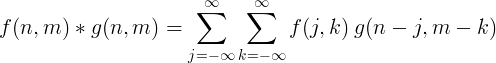
畳み込みによるフィルターの実装
インパルス応答h(n)との畳み込みにより、離散入力信号x(n)をフィルタリングして、出力信号y(n)を取得できます。
y(n)= x(n)* h(n)
畳み込み定理
2つの関数の乗算のフーリエ変換は、各関数のフーリエ変換の畳み込みに等しくなります。
ℱ{ F ⋅ G } =ℱ{ F } *ℱ{ G }
2つの関数の畳み込みのフーリエ変換は、各関数のフーリエ変換の乗算に等しくなります。
ℱ{ f * g } =ℱ{ f }⋅ℱ{ g }
連続フーリエ変換の畳み込み定理
ℱ{ F(T)⋅ G(T)} =ℱ{ F(T)} *ℱ{ G(T)} = F(ω)* G(ω)
ℱ{ F(T)* G(T)} =ℱ{ F(T)}⋅ℱ{ G(T)} = F(ω)⋅ G(ω)
離散フーリエ変換の畳み込み定理
ℱ{ F(N)⋅ G(N)} =ℱ{ F(N)} *ℱ{ G(N)} = F(K)* G(K)
ℱ{ F(N)* G(N)} =ℱ{ F(N)}⋅ℱ{ G(N)} = F(K)⋅ G(K)
ラプラス変換の畳み込み定理
ℒ{ F(T)* G(T)} =ℒ{ F(T)}⋅ℒ{ G(T)} = F(S)⋅ G(S)