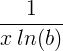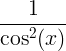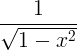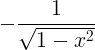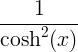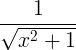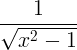微分法則

微分法則と法則。関数テーブルの導関数。

関数の導関数は、Δxが非常に小さい場合の、点x +Δxおよびxでの関数値f（x）とΔxの差の比率です。導関数は、関数の傾きまたは点xでの接線の傾きです。

$f '（x）= \ lim _ {\ Delta x \ to 0} \ frac {f（x + \ Delta x）-f（x）} {\ Delta x}$

二次導関数は次の式で与えられます。

または、単に一次導関数を導出します。

N番目の導関数をf（x）はn回を導出することによって計算されます。

N番目の誘導体では、（N-1）誘導体の誘導体に等しいです。

f ^（n）（x）= [ f ^{（n -1）}（x）] '

の4次導関数を見つける

f（x）= 2 x ⁵

f ^（4）（x）= [2 x ⁵ ] '' '' = [10 x ⁴ ] '' '= [40 x ³ ]' '= [120 x ² ]' = 240 x

関数の導関数は、接線の傾きです。

微分和ルール	（af（x）+ bg（x）） '= af'（x）+ bg '（x）
微分積の法則	（f（x）∙ g（x）） '= f'（x）g（x）+ f（x）g '（x）
微分商の法則	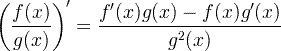$\ left（\ frac {f（x）} {g（x）} \ right） '= \ frac {f'（x）g（x）-f（x）g '（x）} {g ^ 2（バツ）}$
微分連鎖律	f（g（x）） '= f'（g（x））∙ g '（x）

とき、AとBは定数です。

（af（x）+ bg（x）） '= af'（x）+ bg '（x）

次の導関数を見つけます。

3 x ² + 4x。

合計ルールによると：

a = 3、b = 4

f（x）= x ²、g（x）= x

f '（x）= 2 x 、g'（x）= 1

（3 X ² + 4 X）」=3⋅2 X +4⋅1= 6 、X + 4

（f（x）∙ g（x）） '= f'（x）g（x）+ f（x）g '（x）

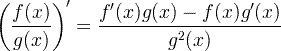
$\ left（\ frac {f（x）} {g（x）} \ right） '= \ frac {f'（x）g（x）-f（x）g '（x）} {g ^ 2（バツ）}$

f（g（x）） '= f'（g（x））∙ g '（x）

この規則は、ラグランジュの表記法でよりよく理解できます。

$\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}$

Δxが小さい場合、f（x ₀）とf '（x ₀）がわかっていると、f（x ₀ +Δx）の近似値を得ることができます。

F（X ₀ +Δ X）≈ F（X ₀）+ F「（X ₀）⋅Δ X