フィボナッチ数とシーケンス

フィボナッチ数列は数の列であり、各数は、0と1である最初の2つの数を除いて、前の2つの数の合計です。

• フィボナッチ数列式
• 黄金比の収束
• フィボナッチ数列表
• フィボナッチ数列計算機
• フィボナッチ関数のC ++コード

フィボナッチ数列式

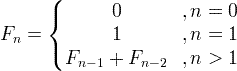
例えば：

F ₀ = 0

F ₁ = 1

F ₂ = F ₁ + F ₀ = 1 + 0 = 1

F ₃ = F ₂ + F ₁ = 1 + 1 = 2

F ₄ = F ₃ + F ₂ = 2 + 1 = 3

F ₅ = F ₄ + F ₃ = 3 + 2 = 5

..。

黄金比の収束

2つの連続するフィボナッチ数の比率は黄金比に収束します。

φは黄金比=（1 +√で5）/ 2≈1.61803399

フィボナッチ数列表

n	F n
0	0
1	1
2	1
3	2
4	3
5	5
6	8
7	13
8	21
9	34
10	55
11	89
12	144
13	233
14	377
15	610
16	987
17	1597年
18	2584
19	4181
20	6765

フィボナッチ数列計算機

未定

フィボナッチ関数のCコード

double Fibonacci(unsigned int n)

{

    double f_n =n;

    double f_n1=0.0;

    double f_n2=1.0;

 

    if( n / 1 ) {

        for(int k=2; k<=n; k++) {

            f_n  = f_n1 + f_n2;

            f_n2 = f_n1;

            f_n1 = f_n;

        }

    }

 

    return f_n;

}