指数法則
指数法則、指数の法則および例。
指数とは
nの累乗で累乗された底aは、aのn倍に等しい:
a n = a × a × ... × a
n回
aは底であり、nは指数です。
例
3 1 = 3
3 2 = 3×3 = 9
3 3 = 3×3×3 = 27
3 4 = 3×3×3×3 = 81
3 5 = 3×3×3×3×3 = 243
指数法則とプロパティ
| ルール名 | ルール | 例 |
|---|---|---|
| 製品ルール | N ⋅ mは= N + M | 2 3 ⋅2 4 = 2 3 + 4 = 128 |
| N ⋅ B N =(⋅ B)nは | 3 2 ⋅4 2 =(3⋅4)2 = 144 | |
| 商の法則 | N / M = N - M | 2 5 /2 3 = 2 5-3 = 4 |
| a n / b n =(a / b)n | 4 3 /2 3 =(4/2)3 = 8 | |
| べき乗則 | (B 、N)、M = B n⋅m | (2 3)2 = 23⋅2 = 64 |
| b n m = b( n m) | 2 3 2 = 2(3 2)= 512 | |
| M √( BのN)= B N / M | 2 √(2 6)= 2 6/2 = 8 | |
| B 1 / N = N √ B | 8 1/3 = 3 √ 8 = 2 | |
| 負の指数 | b -n = 1 / b n | 2 -3 = 1/2 3 = 0.125 |
| ゼロルール | b 0 = 1 | 5 0 = 1 |
| 0 n = 0、n / 0の場合 | 0 5 = 0 | |
| 1つのルール | b 1 = b | 5 1 = 5 |
| 1 n = 1 | 1 5 = 1 | |
| マイナス1つのルール | 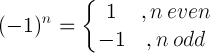 |
(-1)5 = -1 |
| 微分法則 | (X N)' = N ⋅ X N -1 | (X 3)' =3⋅ X 3-1 |
| 積分規則 | ∫ X N DX = X N +1 /(N +1)+ C | ∫ X 2 DX = X 2 + 1 /(2 + 1)+ C |
指数の積の法則
同じベースの積の法則
N ⋅ mは= N + M
例:
2 3 ⋅2 4 = 2 3 + 4 = 2 7 =2⋅2⋅2⋅2⋅2⋅2⋅2= 128
同じ指数の積の法則
N ⋅ B N =(⋅ B)nは
例:
3 2 ⋅4 2 =(3⋅4)2 = 12 2 =12⋅12= 144
参照:指数の乗算
指数の商の法則
同じベースの商の法則
N / M = N - M
例:
2 5 /2 3 = 2 5-3 = 2 2 =2⋅2= 4
同じ指数の商の法則
a n / b n =(a / b)n
例:
4 3 /2 3 =(4/2)3 = 2 3 =2⋅2⋅2= 8
参照:指数の除算
指数のべき乗則
べき乗則I
(N)、M = A n⋅m
例:
(2 3)2 = 23⋅2 = 2 6 =2⋅2⋅2⋅2⋅2⋅2= 64
べき乗則II
a n m = a ( n m)
例:
2 3 2 = 2(3 2)= 2(3⋅3)= 2 9 =2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2= 512
部首によるべき乗則
M √( N)= N / M
例:
2 √(2 6)= 2 6/2 = 2 3 =2⋅2⋅2= 8
負の指数法則
b -n = 1 / b n
例:
2 -3 = 1/2 3 = 1 /(2⋅2⋅2)= 1/8 = 0.125
参照:負の指数