e定数

e定数またはオイラーの数は数学定数です。e定数は実数で無理数です。

e = 2.718281828459 .. ..

eの定義
eのプロパティ
基数e対数
指数関数
オイラーの公式

eの定義

e定数は制限として定義されます。

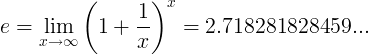
$e = \ lim_ {x \ rightarrow \ infty} \ left（1+ \ frac {1} {x} \ right）^ x = 2.718281828459 .. ..$

代替定義

e定数は制限として定義されます。

$e = \ lim_ {x \ rightarrow 0} \ left（1+ \ right x）^ \ frac {1} {x}$

e定数は、無限級数として定義されます。

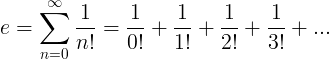
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n！} = \ frac {1} {0！} + \ frac {1} {1！} + \ frac {1} { 2！} + \ frac {1} {3！} + .. ..$

eのプロパティ

eの逆数

eの逆数が限界です：

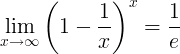
$\ lim_ {x \ rightarrow \ infty} \ left（1- \ frac {1} {x} \ right）^ x = \ frac {1} {e}$

eの導関数

指数関数の導関数は、指数関数です。

（e ^x） '= e ^x

自然対数関数の導関数は、相互関数です。

（log _e x）'=（ln x）' = 1 / x

eの積分

指数関数の不定積分E ^xは、指数関数eである^X。

∫ E ^X DX = E ^X + C

自然対数関数ログの不定積分_E xは次のとおりです。

ログ∫ _E X DX =∫LN X DX = X LN X - X + C

相互関数1 / xの1からeまでの定積分は1です。

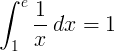
$\ int_ {1} ^ {e} \ frac {1} {x} \：dx = 1$

基数e対数

数xの自然対数は、xの底e対数として定義されます。

ln x = log _e x

指数関数

指数関数は次のように定義されます。

f（x）= exp（x）= e ^x

オイラーの公式

複素数のE ^Iθはアイデンティティを持っています：

電子^Iθ = COS（θ）+ I罪（θ）

iは虚数単位（-1の平方根）です。

θは任意の実数です。

e定数